Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 129

O ar a 0,9 MPa e 400 K entra em um bocal convergente com uma velocidade de 180 m/s. A área da garganta é de 10 cm². Assumindo um fluxo isentrópico, calcule e faça um gráfico da vazão em massa através do bocal, a velocidade de saída, o número Mach de saída e a razão pressão de saída e de estagnação versus a razão entre contrapressão e a pressão de estagnação para o intervalo de contrapressão de 0,9 ≥   P b ≥   0,1   M P a .

Passo 1

Faaaaala aí galerinhaa!! Vamos que vamos?

Vamos assumir que o fluxo neste caso é constante, unidimensional e isentrópico e o ar se comportará como gás ideal !!

Aqui é muito importante nós acharmos a pressão crítica!! Porque para todas as contrapressões inferiores a P * , a pressão no plano de saída do bocal é igual a ela, ou seja:

P e = P *             P b < P *

P e = P b             P b ≥ P *

Então aqui nós já achamos uma forma de calcular a variação da pressão na saída !!

Lembrando que:

P * = P 0 2 k + 1 k k - 1

A temperatura e a pressão de estagnação são dadas por:

T 0 = T 1 + V 1 2 2 c p

P 0 = P 1 T 0 T 1 k k - 1

Para o ar nós temos que:

k = 1,4

c p = 1,005 k J k g . K

R = 0,287 k J k g . K  

E que:

V 1 = 180 m s

P 1 = 900   k P a

T 1 = 400   K

Então:

T 0 = 400   K + 180 m s 2 2 1,005 × 10 3 J k g . K = 416,1   K

P 0 = 900   k P a 416,1   K 400   K 1,4 1,4 - 1 = 1033,3   k P a

E a pressão de estagnação:

P * = 1033,3   k P a 2 1,4 + 1 1,4 1,4 - 1 = 545,9   k P a

Então:

P e = 545,9   k P a             P b < 545,9   k P a

P e = P b             P b ≥ 545,9   k P a

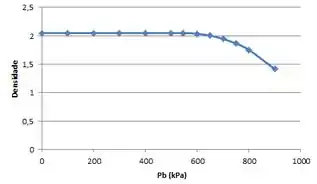
Fazendo um gráfico com essas informações:

Passo 2

A temperatura é dada por:

T e = T 0 P e P 0 k - 1 k

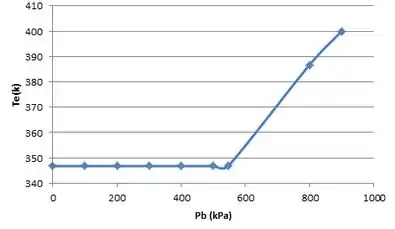
Então:

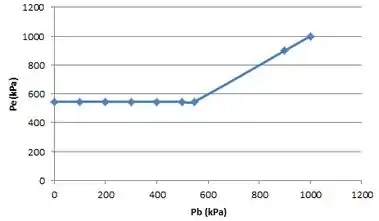
T e = 416,1   K 545,9   k P a 1033,3   k P a 1,4 - 1 1,4               P b < 545,9   k P a

T e = 416,1   K P b 1033,3   k P a 1,4 - 1 1,4               P b ≥ 545,9   k P a

E plotando isso no gráfico:

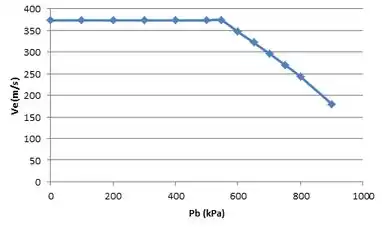
Para a velocidade também basta nós lembramos da fórmula:

V = 2 c ´ p T 0 - T e

Igual fizemos para a anterior:

V = 2 1,005 × 10 3 J k g . K 416,1   K - 346,75   K               P b < 545,9   k P a

V = 2 1,005 × 10 3 J k g . K 416,1   K - T e               P b ≥ 545,9   k P a

E no gráfico:

Passo 3

Para o número Mach:

M a e = V e c e = V e k R T e

Então:

M a e = 373,34 m s 1,4 0,287 × 10 - 3 J k g . K 346,75   K           P b < 545,9   k P a

M a e = V e 1,4 0,287 × 10 - 3 J k g . K T e           P b ≥ 545,9   k P a

E no gráfico:

E para finalizar, a vazão mássica:

m ˙ = ρ e V e A e = P e R T e V e A e

Então:

m ˙ = 545,9 × 10 3 P a 287 J k g . K 346,75   K 373,34 m s 0,001   m 2         P b < 545,9   k P a

m ˙ = P e 287 J k g . K T e V e 0,001   m 2         P b ≥ 545,9   k P a

E assim:

Aguardo vocês na próximaa !!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Narragansett Bay is approximately 21 (statute) mi long andhas an average depth of 42 ft. Tidal charts for the area indicate a time delay of 30 min between high tide at the mouthof the bay (Newport, Rh
Water flows down a rectangular channel that is 4 ft wideand 2 ft deep. The fl ow rate is 20,000 gal/min. Estimate theFroude number of the flow.
It is desired to deliver 30,000 gal/min of water in a brickwork channel laid on a slope of 1:100. Which wouldrequire fewer bricks, in uniform flow: (a) a V channel withθ 5 458, as in Fig. P10.41, or (
The equilateral-triangle channel in Fig. P10.25 has constant slope So and constant Manning factor n. If y 5 a/2,fi nd an analytic expression for the flow rate Q.
An engineer makes careful measurements with a weir (seeSec. 10.7) that monitors a rectangular unfinished concretechannel laid on a slope of 18. She fi nds, perhaps with surprise, that when the water d