Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 88
Qual é o efeito do ganho de aquecimento e perda de calor sobre a entropia do fluido durante o escoamento de Rayleigh?
Passo 1
Essa é uma questão teórica sobre o escoamento de Rayleigh. O escoamento de Rayleigh é o escoamento de um gás ideal através de um duto com área constante que troca de calor. O escoamento é unidimensional (a velocidade do fluido só varia em uma direção), permanente (o escoamento não muda com o tempo) com o atrito entre o tubo e o gás desprezível .
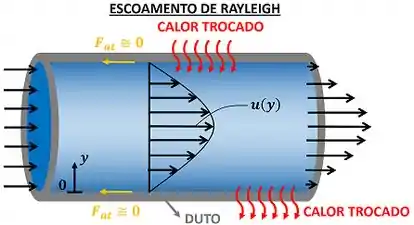
Para estudar escoamento de Rayleigh, usamos um gráfico T-s (temperatura versus entropia) desse escoamento como mostrado abaixo. A curva do gráfico T-s é chamada de linha de Rayleigh. O primeiro passo para descobrir o efeito do aquecimento e da perda de calor sobre a entropia do fluido é entender o que os pontos da linha de Rayleigh significam.
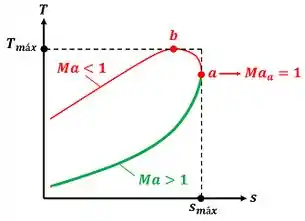
Por isso, veremos no próximo passo o que cada ponto da linha de Rayleigh significa. Depois, no passo 3, podemos explicar melhor o efeito do aquecimento e da perda de calor sobre a entropia .
Passo 2
Nesse passo vamos explicar o que cada ponto da curva de Rayleigh significa.
Para entender isso melhor, vamos imaginar um escoamento de Rayleigh, no qual um gás ideal entra no duto em um estado inicial (com uma pressão , uma temperatura , uma densidade , uma entropia e um número de Mach ). A figura abaixo ilustra essa situação.
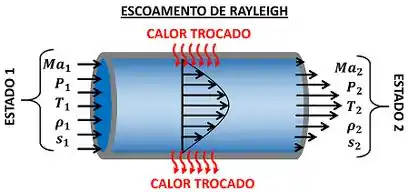
Depois de trocar calor com o ambiente através do duto, o gás sai no estado 2 com uma pressão , uma temperatura , uma densidade , uma entropia e um número de Mach .
Cada estado 1 de entrada do gás gera uma linha de Rayleigh no gráfico T-s.
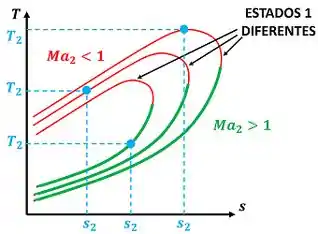
Além disso, vemos pela figura acima que cada ponto da linha de Rayleigh é uma combinação de valores de temperatura final e entropia final que o gás pode ter. Para cada estado 1 de entrada, existem combinações de e diferentes possíveis para o gás.
Os valores possíveis de e são determinados através da aplicação de três leis: a lei de conservação de energia, a lei de conservação de massa e a lei de conservação de quantidade de movimento.
Passo 3
Agora que sabemos o que a linha de Rayleigh significa, podemos entender melhor qual o efeito do aquecimento e do resfriamento sobre a entropia do fluido. Para isso, nós vamos dividir os efeitos em dois casos. Em um caso, o escoamento do gás após a troca de calor (estado 2) é subsônico . Esse caso é marcado com uma linha verde. Em outro caso o escoamento do gás após a troca de calor (estado 2) é supersônico . Esse caso segundo caso é marcado com uma linha verde. A figura abaixo mostra os dois casos.
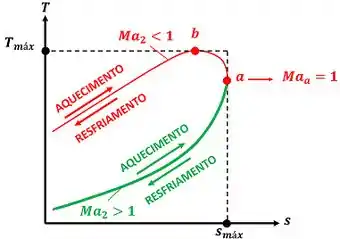
Nós vemos pela figura acima que, para os dois casos ( e ), o aquecimento resulta em um aumento da entropia do fluido até um limite máximo .
Também vemos que, para os dois casos ( e ), o resfriamento resulta em uma diminuição da entropia do fluido.
Resposta
Através da linha de Rayleigh vemos que, para e o aquecimento aumenta a entropia do fluido até um valor máximo e o resfriamento diminui a entropia do fluido.