Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 84

Reconsidere o Problema 12-83. Determine o número de Mach a jusante, a pressão e temperatura abaixo da cunha para um choque oblíquo forte e número de Mach a montante de 5 .

Passo 1

Essa questão é sobre choques oblíquos. No exercício passado nós vimos que o escoamento de ar na parte de cima da cunha sofria expansão. No entanto, o escoamento de ar na parte de baixo da cunha é bloquedo por ela. Isso acaba formando um choque oblíquo forte com ângulo de choque β = β f o r t e . A questão quer saber o número de Mach M a 2 , a pressão P 2 e a temperatura T 2 do ar que atravessou o choque oblíquo forte. A figura abaixo mostra os dados.

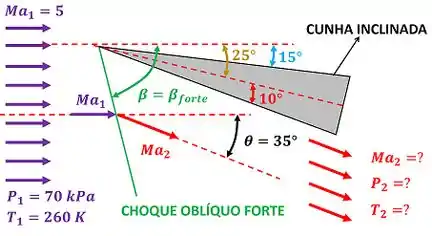
T 1 , P 1 e M a 1 são a temperatura, a pressão e o número de Mach do ar antes de passar pelo choque oblíquo. θ é o ângulo de deflexão do ar. Ou seja, θ é o ângulo que mede o quanto o ar varia de direção, quando atravessa o choque.

T 2 , P 2 e M a 2 dependem do ângulo de choque forte β f o r t e para serem calculdos. Por isso, o nosso próximo passo na resolução do exercício é calcular β f o r t e .

Passo 2

Para achar o valor do ângulo β f o r t e , precisamos de uma equação que nos dê o valor da variável do choque oblíquo que queremos β a partir de termos que já temos, como M a 1 e θ .

A fórmula abaixo faz essa conexão entre termos conhecidos e desconhecidos.

tg ⁡ θ = 2 ⋅ cot ⁡ β ⋅ M a 1 2 ⋅ sen 2 ⁡ β - 1 M a 1 2 ⋅ k + cos ⁡ 2 β + 2

onde k é uma constante que vale 1,4 para o ar.

Apesar da equação de cima relacionar β com termos que conhecemos ( θ e M a 1 ), nós não somos capazes e isolar beta desses dois outros termos para fazer um cálculo direto de β .

Para entender como devemos usar essa fórmula, temos que reorganizá-la.

tg ⁡ θ - 2 ⋅ cot ⁡ β ⋅ M a 1 2 ⋅ sen 2 ⁡ β - 1 M a 1 2 ⋅ k + cos ⁡ 2 β + 2 = 0

Para achar o de β f o r t e a partir da equação acima, vamos precisar variar β entre seu valor mínimo β = 0 até seu valor máximo β = 90 ° . Apenas dois valores de β farão a diferença entre tg ⁡ θ e 2 ⋅ cot ⁡ β ⋅ M a 1 2 ⋅ sen 2 ⁡ β - 1 M a 1 2 ⋅ k + cos ⁡ 2 β + 2 ser igual a zero. O menor desses dois valores não nos interessa, porque é o β f r a c o . O maior valor é o β f o r t e .

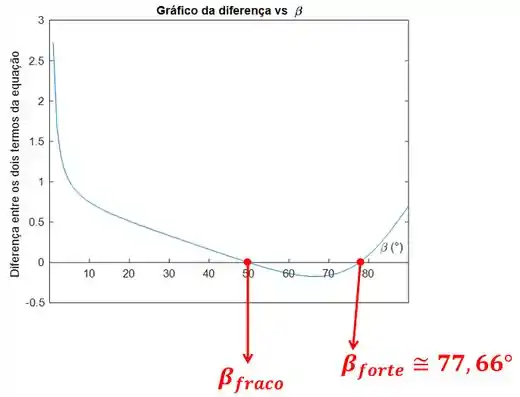
Na figura acima nós vemos que:

β f o r t e ≅ 77,66 °

Esse valor está preciso demais para ser obtido apenas olhando o gráfico e tentando acertar o valor exato do ângulo que corta o eixo x . Essa precisão foi alcançada usando um programa de computador que reconhece os dois valores de β . Esse programa faz justamente o que foi dito antes: varia β até encontrar o maior valor de β que corta o eixo x .

Passo 3

Nesse passo, vamos calcular o valor de número de Mach M a 2 para quando o choque é forte β f o r t e ≅ 77,66 ° . Para isso, precisamos usar a fórmula de choque oblíquo que nos dá os valores de M a 2 a partir do M a 1 . Essa equação se encontra abaixo.

M a 2 , n = k - 1 ⋅ M a 1 , n 2 + 2 2 ⋅ k ⋅ M a 1 , n 2 - k + 1

onde M a 1 , n e M a 2 , n são os números de Mach perpendiculares ao choque oblíquo. A figura abaixo mostra melhor o que são esses números de Mach.

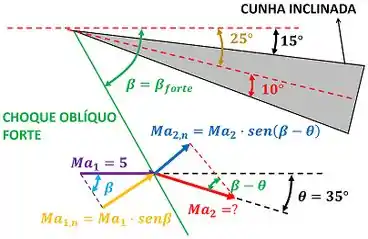
Através da imagem podemos ver que existe uma relação entre M a 1 , n e M a 1 e outra entre M a 2 , n e M a 2 .

M a 1 , n = M a 1 ⋅ sen ⁡ β

M a 1 , n = M a 1 ⋅ sen ⁡ β f o r t e

M a 1 , n = 5 ⋅ sen ⁡ 77,66 °

M a 1 , n = 4,88 5

M a 2 , n = M a 2 ⋅ sen ⁡ β - θ

M a 2 , n = M a 2 ⋅ sen ⁡ β f o r t e - θ

M a 2 , n = M a 2 ⋅ sen ⁡ 77,66 ° - 35

M a 2 , n = M a 2 ⋅ 0,67765

Para β f o r t e M a 2 , n vale:

M a 2 , n = k - 1 ⋅ M a 1 , n 2 + 2 2 ⋅ k ⋅ M a 1 , n 2 - k + 1

M a 2 , n = 1,4 - 1 ⋅ 4 , 88 5 2 + 2 2 ⋅ 1,4 ⋅ 4 , 885 2 - 1,4 + 1

M a 2 , n = 0 , 4169

Isso quer dizer que o M a 2 para β f o r t e vale:

M a 2 , n = M a 2 ⋅ sen ⁡ β f o r t e - θ

0,4169 = M a 2 ⋅ 0,67765

M a 2 = 0,615

Passo 4

Nesse passo, vamos calcular o valor da pressão do ar após o choque P 2 para o choque forte β f o r t e ≅ 77,66 ° . Para isso, precisamos usar a fórmula de choque oblíquo que nos dá os valores de P 2 a partir do P 1 . Essa equação se encontra abaixo.

P 2 P 1 = 2 ⋅ k ⋅ M a 1 , n 2 - k + 1 k + 1         ⟹       P 2 = P 1 ⋅ 2 ⋅ k ⋅ M a 1 , n 2 - k + 1 k + 1

Para β f o r t e P 2 vale:

P 2 = 7 0 ⋅ 2 ⋅ 1,4 ⋅ 4,88 5 2 - 1,4 + 1 1,4 + 1       ⟹       P 2 = 1937   k P a

Passo 5

Nesse passo, vamos calcular o valor da temperatura do ar após o choque T 2 para o choque forte β f o r t e ≅ 86,11 ° . Para isso, precisamos usar a fórmula de choque oblíquo que nos dá os valores de T 2 a partir do T 1 . Essa equação se encontra abaixo.

T 2 T 1 = 2 + k - 1 ⋅ M a 1 , n 2 ⋅ 2 ⋅ k ⋅ M a 1 , n 2 - k + 1 k + 1 2 ⋅ M a 1 , n 2

T 2 = T 1 ⋅ 2 + k - 1 ⋅ M a 1 , n 2 ⋅ 2 ⋅ k ⋅ M a 1 , n 2 - k + 1 k + 1 2 ⋅ M a 1 , n 2

Para β f o r t e T 2 vale:

T 2 =   26 0 ⋅ 2 + 1,4 - 1 ⋅ 4,88 5 2 ⋅ 2 ⋅ 1,4 ⋅ 4,88 5 2 - 1,4 + 1 1,4 + 1 2 ⋅ 4,88 5 2         ⟹       T 2 = 1450   K

Resposta

M a 2 = 0,615

P 2 = 1937   k P a

T 2 = 1450   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o software EES e as relações na Tabela A – 13, calcule as funções unidimensionais de fluxo compressível para um gás ideal com k = 1.667 e apresente seus resultados duplicando a Tabela A – 13.
O hélio se expande em um bocal de 1 MPa, 500 K e velocidade desprezível para 0,1 MPa. Calcule as áreas da garganta e de saída para uma taxa de fluxo em massa de 0,25 k g s , assumindo que o bico seja
Usando o software EES e as relações na Tabela A – 14, calcule as funções unidimensionais de fluxo compressível para um gás ideal com k = 1.667 e apresente seus resultados duplicando a Tabela A – 14.
Um avião voa com um número Mach M a 1 = 0,8 a uma altitude de 7000 m, na qual a pressão é de 41,1 kPa e a temperatura é de 242,7 K. O difusor na entrada do motor tem um número Mach de saída M a 2 = 0
O nitrogênio entra em um bocal convergente-divergente a 700 kPa e 300 K com uma velocidade desprezível e sofre um choque normal em um local onde o número Mach é M a =3 , 0 Calcule a pressão, temperatu