Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 117

13-117 Água escoando em um canal horizontal largo se aproxima de uma saliência com 20 cm de altura a uma velocidade de 1,25 m/s e profundidade de escoamento de 1,8 m. Determine a

velocidade, a profundidade de escoamento e o número de Froude sobre a saliência.

Passo 1

Vamos láaa!!!

A gente quer velocidade V 2 , a profundidade de escoamento y 2 e o número de Froude em cima da saliência F r 2 !

Vamos começar calculando o número de Froude antes da saliência:

F r 1 = V 1 g y 1   = 1,25 9,81 × 1,8 = 0,297

O escoamento é subcrítico antes da saliência, então esperamos que o escoamento seja estrangulado!

Podemos achar a profundidade y 2 usando a equação de energia, mas primeiro precisamos conhecer a energia específica a montante:

E s 1 = y 1 + V 1 2 2 g = 1,8 + 1,25 2 2 × 9,81 = 1,88   m

Passo 2

Usando a equação de energia:

y 2 3 - E s 1 - Δ z b y 2 2 + V 1 2 2 g y 1 2 = 0

Substituindo:

y 2 3 - 1,88 - 0,20 y 2 2 + 1,25 2 × 9,81 × 1,80 2 = 0

Vamos precisar da ajuda do solver do excel!

Colocando todos os dados temos:

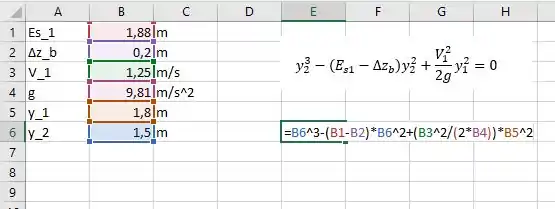
Como y 1 = 1,8 e Δ z b = 0,20 então y 2 deve ser menor que 1,6   m . Com um chute de y 2 = 1,5 m usamos o solver e achamos:

y 2 = 1,576   m

Passo 3

Agora que a gente conhece y 2 , podemos achar V 2 usando a equação de continuidade:

V 2 = y 1 y 2 V 1 = 1,8 1,576 × 1,25  

Calculando:

V 2 = 1,43   m / s

Passo 4

Só falta o número de Froude!! Para isso vamos usar:

F r 2 = V 2 g y 2 = 1,43 9,81 × 1,576

Calculando:

F r 2 = 0,363

Aweeeee!!!

Resposta

V 2 = 1,43   m / s

y 2 = 1,576

F r 2 = 0,363

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Water flows down a rectangular channel that is 4 ft wideand 2 ft deep. The fl ow rate is 20,000 gal/min. Estimate theFroude number of the flow.
It is desired to deliver 30,000 gal/min of water in a brickwork channel laid on a slope of 1:100. Which wouldrequire fewer bricks, in uniform flow: (a) a V channel withθ 5 458, as in Fig. P10.41, or (
The equilateral-triangle channel in Fig. P10.25 has constant slope So and constant Manning factor n. If y 5 a/2,fi nd an analytic expression for the flow rate Q.
An engineer makes careful measurements with a weir (seeSec. 10.7) that monitors a rectangular unfinished concretechannel laid on a slope of 18. She fi nds, perhaps with surprise, that when the water d
A trapezoidal channel has n 5 0.022 and S0 5 0.0003 andis made in the shape of a half-hexagon for maximumefficiency. What should the length of the side of the hexagon be if the channel is to carry 225