Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 102
Considere o escoamento da água em um reservatório de soleira espessa com 0,80 m de altura e suficientemente longo. Se a profundidade mínima de escoamento acima do reservatório for medida como 0,50 m, determine a vazão por metro de largura no canal e a profundidade de escoamento a montante do reservatório.
Passo 1
Bora começar a questão desenhando um esqueminha??!!
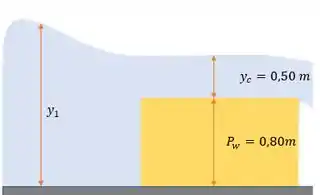
Queremos achar a vazão por metro de largura, e a profundidade do canal antes do reservatório, !
Sabendo que a profundidade do escoamento acima do reservatório mínima quando é crítica, podemos usar a seguinte expressão:
Passo 2
Conhecemos todas as variáveis menos a vazão, que é quem queremos encontrar, então podemos isolar :
Como queremos a vazão por metro de largura, então :
Awee, achamos a vazão, agora vamos atrás do !!
Passo 3
O aparece nessa equação aqui ó:
O problema é que não conhecemos , então vamos pensar onde mais o aparece...
Temos o coeficiente de descarga:
Mas não conhecemos , por sua vez o coeficiente de descaga aparece na expressão para vazão:
Podemos substituir e ficamos com:
Substituindo os dados:
Opaa, continha difícil né!! Vamos pedir a ajuda do solver do excel!
Passo 4
Para isso vamos igualar a equação a zero e como , vamos chutar que , vai ficar assim:
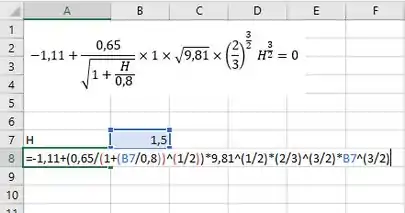
Usando o solver, achamos . Agora sim podemos achar !!!
Substituindo:
Aweeee!!!!