Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 14.Problemas - Ex. 77

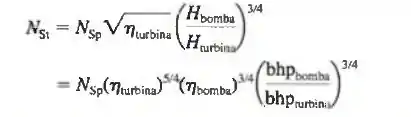
14-76 Considere uma bomba-turbina que opera tanto como bomba quanto como turbina. Sob condições nas quais a velocidade rotacional ω e a vazão V ˙   são iguais para a bomba e a turbina, verifique se as velocidades específicas da turbina e da bomba estão relacionadas como:

Passo 1

Opaaa, ei ai!? Tudo show de bola?!

A gente tem uma máquina que funciona tanto como bomba quanto turbina e ω   e V ˙ são iguais para as duas funções.

A gente tem relacionar a velocidade específica da bomba e da turbina e chegar na mesma expressão que o problema deu pra a gente!

Vamos lembrar algumas formulinhas, primeiro a velocidade específica da bomba:

N S p = ω V ˙ 1 2 g H B o m b a 3 4  

A velocidade específica da turbina:

N S t = ω b p h T u r b i n a 1 / 2 ρ 1 / 2   g H T u r b i n a 3 / 4

Show, agora vamos rearranjar a velocidade específica da turbina de uma forma que a expressão de eficiência da turbina apareça!

Lembrando a fórmula de η T u r b i n a :

η T u r b i n a = b p h T u r b i n a ρ g H T u r b i n a V ˙

Dando aquela arrumadinha a gente fica assim:

N S t = ω V ˙ 1 2 g H T u r b i n a     3 4   b p h T u r b i n a ρ g H T u r b i n a V ˙ 1 / 2

Podemos substituir a eficiência:

N S t = ω V ˙ 1 2 g H T u r b i n a     3 4   η T u r b i n a 1 / 2

Passo 2

Vamos dar uma olhadinha nas eficiências da bomba e da turbina juntas:

η T u r b i n a = b p h T u r b i n a ρ g H T u r b i n a V ˙

η B o m b a = ρ g H B o m b a V ˙ b p h B o m b a

A vazão é a mesma, portanto:

H T u r b i n a = H B o m b a b h p T u r b i n a b h p B o m b a   η B o m b a η T u r b i n a

A gravidade de a densidade do fluido a gente cortou no processo!

Agora vamos pegar esse H T u r b i n a e vamos substituir lá na expressão de velocidade específica da turbina que a gente tinha deixado no jeito:

N S t = ω V ˙ 1 2 g H B o m b a     3 4   η T u r b i n a 1 2 b h p B o m b a   η B o m b a η T u r b i n a b h p T u r b i n a 3 / 4

Agora é só arrumar a casa:

N S t = N S p   η T u r b i n a 5 4   η B o m b a 3 4   b h p B o m b a   b h p T u r b i n a 3 / 4

Aweee!!!

Passo 3

Se a gente substituir os b h p s usando as fórmulas de eficiência, chegamos em:

N S t = N S p   η T u r b i n a 5 4   η B o m b a 3 4   ρ g H B o m b a V ˙ η B o m b a ρ g H T u r b i n a V ˙ η T u r b i n a 3 / 4

Agora organizamos e:

N S t = N S p   η T u r b i n a 1 2     H B o m b a H T u r b i n a 3 / 4

Prontinho!!!

Resposta

N S t = N S p   η T u r b i n a 5 4   η B o m b a 3 4   b h p B o m b a   b h p T u r b i n a 3 / 4

N S t = N S p   η T u r b i n a 1 2     H B o m b a H T u r b i n a 3 / 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14-85 A turbina-protótipo correspondente a uma turbina-modelo era escala um para cinco discutida no Problema 14-84 deve operar através de uma carga líquida de 50 m. Determine a rpm e a vazão apropriad
14-86 Prove que a turbina-modelo (Problema 14-84) e a turbina-protótipo (Problema 14-85) operam a pontos homólogos, comparando a eficiência da tuibina e a velocidade específica daturbina em ambos os c
14-89 Calcule e compare a eficiência das duas turbinas do Problema 14-88. Elas devem ser iguais, uma vez que estamos assumindo a semelhança dinâmica. Entretanto, a turbina maior, na verdade, será lige
14-83 Calcule a velocidade específica da tuibina do Problema 14-63. Forneça respostas nas formas adimensionais e em unidades padrão dos EUA. Elas estão no intervalo normal de uma turbina Francis? Caso
Calcule e compare a eficiência das duas turbinas do Problema 14-100. Elas devem ser iguais, uma vez que estamos considerando a semelhança dinâmica. Entretanto, a turbina maior, na verdade, será ligeir