Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 174

174 – Uma parede de 4   m e 6   m de comprimento é construída por duas grandes placas grossas de aço k = 15 W m ⋅ K de 2   c m de espessura, separadas por barras de aço de 1   c m de espessura e 22   c m de largura colocadas com 99   c m de intervalo. O espaço restante entre as placas de aço é preenchido com isolante de fibra de vidro k = 0,035 W m ⋅ K . Considerando que a diferença de temperatura entre as superfícies interna e externa das paredes é 22   ℃ , determine a taxa de transferência de calor através da parede. Será que podemos ignorar as barras de aço entre as chapas na analisa da transferência de calor, uma vez que ocupam apenas 1 % da área de transferência de calor?

Passo 1

Dados fornecidos:

Área da parede de aço,  A i = 6 × 4 = 24   m 2

Espessura das chapas de aço,  t 12 = t 34 = 0,8   c m = 0,008   m

Espessura das chapas de aço,  t 23 = 22   c m = 0,22   m

Espessura do isolamento de fibra de vidro,  t 23 = 22   c m = 0,22   m

Comprimento do isolamento de fibra de vidro,  L A = 99   c m = 0,99   m

Comprimento da chapa de aço,  L B = 1   c m = 0,01   m

Condutividade térmica das chapas de aço,  k = 15 W m ⋅ K

Condutividade térmica do isolamento,  k = 0,035 W m ⋅ K

Diferença de temperatura entre as superfícies interna e externa da parede,  ∆ T = 22   ℃ .

Passo 2

Vamos resolver essa questão considerando o cálculo de uma porção de 1 m   de altura e 1   m de largura de parede, ou seja, um fluxo de transferência de calor q ˙ .

As resistências entre as duas temperaturas podem ser visualizadas na ilustração abaixo:

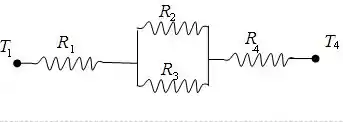
Usando a abordagem de rede térmica, a resistência total da rede pode ser determinada como:

R t o t a l = R 1 + R 23 + R 3

= R 1 + R 2 R 3 R 2 + R 3 + R 4

Temos que:

R 1 = t 12 k f e r r o A 0

R 2 = t 23 k i s o l a n t e A i

R 3 = t 23 k f e r r o A b

R 23 = R 2 R 3 R 2 + R 3 = t 23 k i s o l a n t e A i t 23 k f e r r o A b t 23 k i s o l a n t e A i + t 23 k f e r r o A b

R 4 = t 34 K f e r r o A o

Temos a resistência total como:

R t o t a l = t 12 k f e r r o + t 23 k i s o l a n t e A i t 23 k f e r r o A b t 23 k i s o l a n t e A i + t 23 k f e r r o A b + t 34 K f e r r o A o

Onde:

A 0 = 1   m ²

A i = 0,99   m ²

A b = 0,01   m ²

Passo 3

A resistência total se multiplica  A i = A o = ( L A + L B ) e pode ser expressa como:

R t o t a l = t 12 k f e r r o A 0 + t 23 k i s o l a n t e A i t 23 k f e r r o A b t 23 k i s o l a n t e A i + t 23 k f e r r o A b + t 34 K f e r r o A o

= t 12 k f e r r o A 0 + t 23 k i s o l a n t e ⋅ L A t 23 k f e r r o ⋅ L B t 23 k i s o l a n t e ⋅ L A + t 23 k f e r r o ⋅ L B + t 34 K f e r r o A o

Substituindo pelos valores fornecidos no “Passo 1”, temos:

= 0,008   m 15 W m ⋅ K 1   m ² + 0,22 0,035 × 0,99 × 0,22 15 × 0,01 0,22 0,035 × 0,99 + 0,22 15 × 0,01 + 0,008   m 15 W m ⋅ K 1   m ²

= 1,1925   m 2 ⋅ K W

E o fluxo de calor é:

q ˙ = ∆ T R t o t a l = 22   ℃ 1,1925   m 2 ⋅ K W = 18,45 W m ²

Passo 4

A taxa média de calor através da parede pode ser determinado como:

Q ˙ = A q ˙

Q ˙ = 24   m ² × 18,45 W m ²

Q ˙ = 442,8   W

Passo 5

Vamos calcular a transferência total de calor através da parede, negligenciando as barras de aço entre as placas,

A i = A 0

R t o t a l A i = t 12 k f e r r o + t 23 k i s o l a n t e + t 34 k f e r r o

= 0,008 15 + 0,22 0,035 + 0,008 15

= 6,29 m 2 ⋅ K W

O fluxo médio de calor através da parede pode ser determinado como:

q ˙ = Q ˙ A i

= T 4 - T 1 R t o t a l A i

= 22 6,29

= 3,496   W / m 2

A transferência total de calor através da parede composta pode ser determinada como:

Q ˙ = A q ˙

= 24 × 3,496

= 83,904   W

Como negligenciamos as barras de aço entre duas chapas de aço, a taxa total de transferência de calor reduziu drasticamente e o erro deve ser

% E r r o = 442,8   - 83,904 442,8   W × 100

= 81,05   %

Portanto, embora tenhamos ignorado 1% da área total, o erro é significativo e, portanto, não podemos ignorar as barras de aço para o cálculo. 81% da transferência total de calor ocorre através das barras de aço na parede, apesar do espaço insignificante que elas ocupam. As barras de conexão estão servindo como "pontes térmicas"

Resposta

Q ˙ = 442,8   W

Embora tenhamos ignorado 1% da área total, o erro é significativo e, portanto, não podemos ignorar as barras de aço para o cálculo. 81% da transferência total de calor ocorre através das barras de aço na parede, apesar do espaço insignificante que elas ocupam. As barras de conexão estão servindo como "pontes térmicas"

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma parede de 25 cm de espessura, 9 m de comprimento e 3 m de altura deve ser construída com tijolos k = 0,70 W m . K sólidos de 18c m × 18c m ou tijolos de dimensões idênticas com nove buracos de ar
Uma parede de 10 cm de espessura deve ser construída com vigas de madeira k = 0,11 W m . K de 2,5 m de comprimento com seção transversal de 10c m × 10c m . Em algum momento, o construtor ficou sem as
Repita o problema anterior considerando que a resistência térmica de contato nas interfaces D-F e E-F seja 0,00012 m 2 ° C W .
Uma parede de 4 m de altura e 6 m de largura consiste de tijolos k = 0,72 W m . K horizontais com seção transversal de 15c m ×25c m separados por camada de gesso k = 0,22 W m . K de 3 cm de espessura.
Uma parede de 12 m de comprimento e 5 m de altura é construída com duas camadas de 1 cm de espessura de placa de gesso reforçada k = 0,17 W m . K espaçadas de 16 cm por vigas de madeira k = 0,11 W m .