Uma parede de 12 m de comprimento e 5 m de altura é construída com duas camadas de 1 cm de espessura de placa de gesso reforçada espaçadas de 16 cm por vigas de madeira cuja seção transversal é . As vigas são colocadas verticalmente com 60 cm de intervalo, e o espaço entre elas é preenchido com isolante de fibra de vidro . A casa é mantida a 20°C e a temperatura ambiente externa é de -9°C. Tomando os coeficientes de transferência de calor nas superfícies interna e externa da casa como sendo e , respectivamente, determine:
- A resistência térmica da parede considerando uma seção representativa;
- A taxa de transferência de calor através da parede.
Passo 1
Bora lá galera, vamos desenhar:
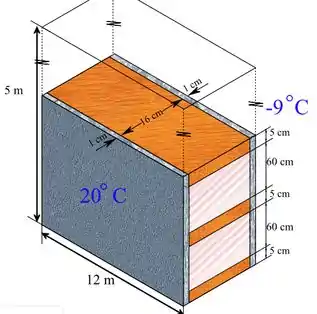
Para começar nós vamos desenhar as resistências, como a estrutura interna da parede se repete vamos analisar somente a resistência da madeira e do isolante, depois estendemos para o restante da parede!!
Se já entendemos isso, na letra a, nossa área representativa será referente aos 5 cm da madeira e 60 cm do isolante de altura e 1 m do comprimento, ou seja:
Bora desenhar:

Legal, pelo esquema nós vemos que estão em paralelo entre si, então:
Que está em sequencia com as demais:
Até aqui tudo certo ?
Passo 2
Agora vamos calcular cada resistência separadamente, ok?
Relembrando os dados:
Bom galera quando estamos calculando a resistência convectiva e para o gesso nós podemos usar a área representativa, certo?
No caso da madeira, já não temos mais uma altura de 65 cm, mas sim de 5 cm, não é? Então neste caso a área será de :
No caso da área do isolante teremos
E quanto a resistência total? Bora substituir né?
Já achamos a resistência total, agora só precisamos do fluxo de calor!!
Passo 3
Na letra b nós precisamos da taxa de transferência de calor pela parede.
Se lembram de como calcular o calor?
Fácil, não é?
Substituindo:
Como a variação em graus Celsius é a mesma que a variação em kelvin:
Como estamos analisando um espaço referente a 0,65 m de altura e 1 m de largura:
Como a cada intervalo de a estrutura da parede se repete, para a parede total de 12 m de comprimento e 5 m de altura a troca total de calor será:
E é isso aí galera !!