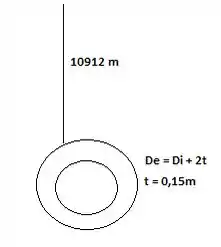
Em 1960, o batiscafo Trieste de Auguste e Jacques Picard bateu um recorde descendo a uma profundidade de 10912 m no Oceano Pacífico, próximo de Guam. A esfera que alojava o passageiro tinha 2,1 m de diâmetro, 15 cm de espessura e uma janela com 40 cm de diâmetro. (a) Calcule a força hidrostática sobre a janela naquela profundidade. (b) Se a janela for vertical, a que distancia abaixo do seu centro está o centro de pressão?

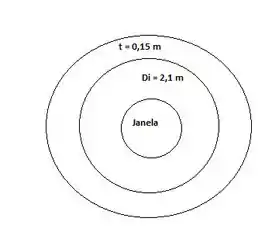
(b)Para a janela na vertical, seu muda em relação a letra (a), uma vez que agora estaremos mais profundo, tal que esse novo valor será o valor da profundidade somado ao valor da espessura da esfera com o valor do raio interno da esfera e o raio da janela.

Para uma esfera o seu centro de pressão será dado por:

O centro de pressão se manteve basicamente no mesmo lugar de quando estava na parte superior.