Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 129
Reconsidere o Problema 3-128. Usando o EES (ou outro aplicativo), investigue o efeito da pressão do ar acima da água sobre a força no cabo. Faça a pressão variar de 0,1 MPa até 10 MPa. Represente graficamente a força do cabo versus a pressão do ar.
Passo 1
Vamos relembrar a questão anterior com esse esqueminha aqui!
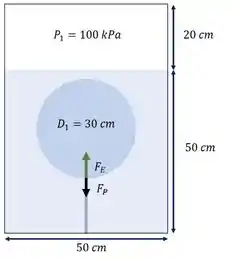
Temos um balão preso por um cabo, dentro de um tanque fechado e cheio de água, o cabo faz uma força , dada por:
O diâmetro do balão varia de acordo com a pressão do ar na superfície livre da água(), a partir da seguinte relação:
Onde é uma constante desconhecida e é o diâmetro do balão.
A variação percentual de é dada por:
Onde é a força do cabo inicial, igual a e vai variar de até .
Na resolução da quentão anterior, achamos a seguinte relação:
Ela vai ser bastante útil pra a gente!
Passo 2
Agora vamos substituir a expressão de na expressão de percentual:
Onde é o diâmetro incial igual a ou e é o diâmetro que vai variar. Arrumando a equação, temos:
Cortando o que a gente pode cortar, temos:
Agora vamos voltar rapidinho nessa relação que achamos na resolução anterior:
Nesse caso é o diâmetro do balão quando a pressão é , a mesma coisa vale para e . Para usar essa expressão aqui vamos dar outro significado para e , aqui ao invéz deles serem costantes eles vão ser variáveis.
Vamos dar uma arrumadinha para poder substituir essa relação na expressão do percentual:
Substituindo, temos:
Arrumando:
Prontinho! Agora temos uma expressão que relaciona a variação da força com a variação de pressão!
Passo 3
Agora que temos todos os dados e as relações que a gente vai precisar, só precisamos passar isso para o EES, constuir a tabela e plotar o gráfico!
Com o EES aberto, vamos colocar os dados e as funções, vai ficar assim:
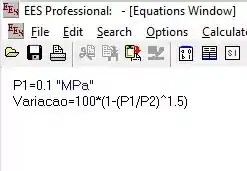
Agora fazemos a tabela escolhendo as variáveis e :
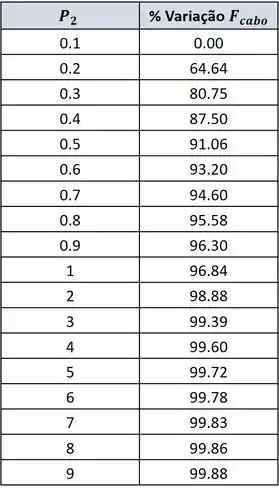
Plotando o gráfico com no eixo e no eixo .
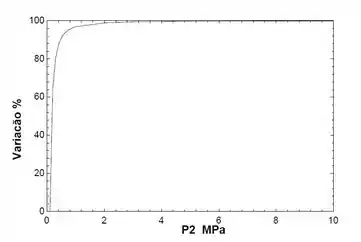
Resposta
Ei, a resposta está no passo a passo :)