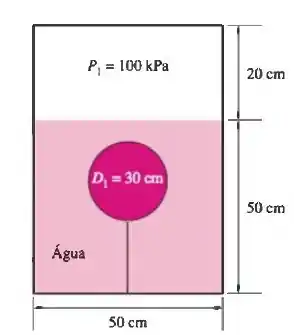
Um balão de ar elástico com diâmetro de 30 cm é acoplado à base de um contêiner parcialmente preenchido com água a , como mostra a Figura. Se a pressão do ar

acima da água aumentar gradualmente de 100 kPa até 1,6 MPa, a força no cabo variará? Nesse caso, qual é a variação percentual da força? Suponha que a pressão na superfície livre e o diâmetro do balão estejam relacionados por , onde C é uma constante e n = -2 . O peso do balão e do ar que há nele são desprezíveis.

Pra a gente visualizar melhor, olha só esse esqueminha:

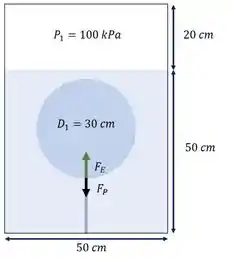
Aqui é a força peso do balão, que o enunciado disse que é desprezível, ele só ta aqui pra a gente visualizar melhor, ok? E é a força de flutuação do balão e é dada por:

Onde é a aceleração da gravidade e é o volume dado por:

A força do cabo é dada por:

Mas como a gente vai desconsiderar , temos:

Temos esses dados, então bora substituir e calcular!

Calculando:

Não comecemos o diâmetro do balão quando a pressão é e precisamos dele pra calcular , então para isso vamos precisar usar essa relação aqui:

Fazendo:

E:

Como não conhecemos podemos dividir uma expressão pela outra, pra poder cancelar o ! Beleza?

Arrumando, temos:

Substituindo:

Calculando:

Agora podemos calcular a força do cabo para esse diâmetro:

Calculando:

Agora que conhecemos as duas as duas forças, podemos calcular a variação percentual da força, fezendo:

Substituindo:

Calculando:

Achamos nosso percentual de variação da força!!