Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 131
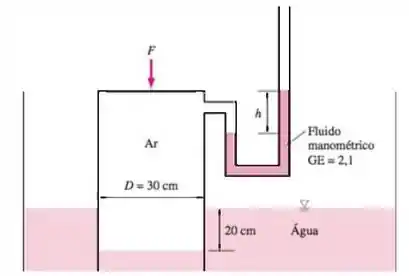
Um contêiner cilíndrico cujo peso é de 79 N é invertido e pressionado na água, como mostra a Figura. Determine a altura diferencial h do manômetro e a força F necessária para
manter o contêiner na posição mostrada.
Passo 1
Pra começar com o pé direito, vamos olhar um esqueminha!
A gente tem um contêiner cilindrico com diâmetro , com submerso na água! Vamos considerar densidade da água é e a gravidade . Não sabemos a altura do manômetro e a densidade relativa do fluido é . Vamos começar achando a densidade do fluido!
A questão ta pedindo a altura do manômetro e força necessária para que o contêiner fique nessa posição.
Passo 2
Vamos começar achando o !
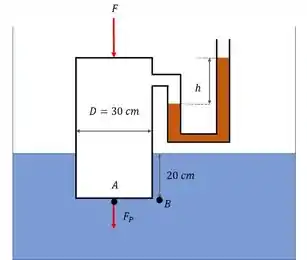
A altura do manômetro diz pra a gente a pressão no ponto A, conforme mostra essa expressão:
Mas não temos nem nem ! Para resolver isso, vamos pegar o ponto B, que esta na mesma altura que o ponto A. Sabendo que tanto no ponto A, quanto no ponto B o fluido é o mesmo, temos:
Podemos calcular
é a altura de água em que o contêiner esta afundado, o enunciado da ele em , precisamos passar para !! Substituindo, temos:
Calculando:
Como as pressões são iguais, podemos achar agora!
Calculando:
Ou:
Achamos a altura!!!
Passo 3
Agora para achar a força temos que fazer o balanço das forças, para isso vamos dar outra olhadinha no nosso esquema:
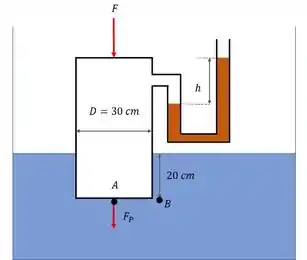
Temos 3 forças agindo sobre o contêiner, a força peso , dada pelo enunciado. A força que é a força que queremos achar e a força de flutuação que é a força apontando para cima. Para que o contêiner fique nessa posição, essas forças tem que estar em equilibrio. Então temos:
A força de flutuação é dada por:
E:
Substituindo:
Se observarmos, vemos que:
Como já esta calculado, só precisamos de
Finalmente:
Agora vamos voltar ao equilíbrio das forças, substituit e isolar :
Substituindo:
Calculando:
Resposta
A altura do manômetro é: e a força é .