Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 7
Ar a 20°C e 1 atm entra em um duto quadrado de 40 cm, como mostra a Figura P7.7. Aplicando o conceito de “espessura de deslocamento” da Figura 7.4, determine
(a) a velocidade média e (b) a pressão média no núcleo do escoamento na posição x =3 m. (c) Qual o gradiente de pressão médio, em Pa/m, nessa seção?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos ar a e entrando em um duto quadrado de base , com a velocidade da corrente livre (a que entra no sistema) de como demonstra a figura que ilustra o problema.
O enunciado nos pede então para aplicar o conceito de “espessura de deslocamento”, no qual num escoamento sobre uma placa linhas de corrente externas devem defletir para fora a uma distância a fim de satisfazer a conservação da massa entre a entrada e a saída.
Nos próximos passos, vamos utilizar esse conceito para calcular a velocidade média do escoamento na saída da placa, , a pressão média no núcleo do escoamento em e o gradiente de pressão nesta mesma seção.
Além disso, devemos lembrar que para ar a a massa específica é .
Então vem comigo que a gente vai resolver esse problema!
Passo 2
Pra começar, vamos resolver a letra (a).
Em primeiro lugar, vamos calcular o número de Reynolds do escoamento na posição :
E isso caracteriza um escoamento laminar para uma placa plana, pois o número de Reynolds está na faixa .
Agora podemos calcular o deslocamento da camada limite a partir da Equação (7.13), fornecida na página 467:
Por fim, devemos calcular a velocidade na saída.
Se você prestar atenção na figura que ilustra o problema, vai ver que a área da seção transversal do escoamento é diferente na entrada e na saída do duto por conta do deslocamento da camada limite.
Veja esse esquema pra entender:
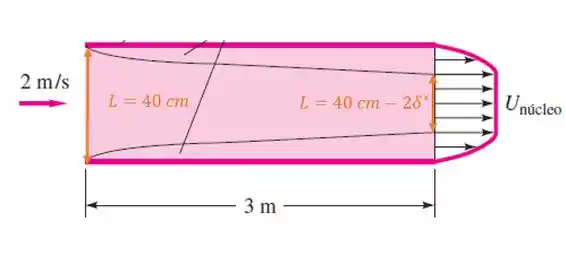
Como vocês podem ver na imagem, na saída o comprimento do lado da base quadrada deve levar em conta o deslocamento da camada-limite, e por isso ele será de .
Podemos então usar a equação da continuidade para calcular a velocidade na saída:
Passo 3
Agora vamos resolver a letra (b).
Pra calcular a pressão na saída do duto ou seja, onde , basta que a gente use a Equação de Bernoulli.
Vamos considerar a pressão na entrada como sendo e iremos calcular a pressão manométrica, ou seja, .
Dessa maneira:
Passo 4
Pra finalizar a questão, vamo resolver a letra (c).
Pra calcular o gradiente de pressão, basta que a gente divida a variação de pressão total (manométrica) pelo comprimento do duto, ou seja, .
Dessa maneira:
Pronto, matamos a questão juntos!
Resposta
(a) A velocidade média no fim da placa é
(b) A pressão média no núcleo do escoamento no fim da placa é
(c) O gradiente de pressão médio no duto é