Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 7.Problemas - Ex. 65
Seja o sistema do Problema 4.54. A superfície interna está exposta a gases quentes a 350°C, com um coeficiente de transferência de calor por convecção de 100 W/(m2 K), enquanto há convecção na superfície externa com ar a 25°C e um coeficiente de transferência de calor por convecção de 5 W/(m2 - K).
a) Usando uma malha com espaçamento de 75 mm, calcule o campo de temperaturas no interior do sistema e determine a perda de calor por convecção para o ar, na sua superfície externa do canal, por unidade de comprimento. Compare esse resultado como calor ganho por convecção a partir dos gases quentes na superfície interna.
(b) Determine o efeito do espaçamento da malha no campo de temperaturas e na perda de calor para o ar, por unidade de comprimento. Especificamente, considere um espaçamento na malha de 25 mm e represente isotermas apropriadamente espaçadas em um esboço do sistema, avalie os efeitos de mudanças nos coeficientes de transferência de calor por convecção no campo de temperaturas e na perda de calor.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Bem, o que é que a gente sabe? Sabemos que: Conduto de seção transversal quadrada com geometria prescrita, condutividade térmica e condições convectivas de superfície interna e externa.
E temos que encontrar: (a) Perda de calor por unidade de comprimento, q , por convecção para o ar, (b) Efeito do espaçamento da grade e coeficiente de convecção do campo de temperatura; mostrar isotermas.
Show. Saca esse esquemático:
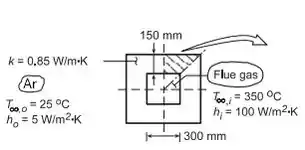
Para o item (a) Aproveitando a simetria, a rede nodal para um espaçamento de grade de 75 mm é mostrada no esquema abaixo:
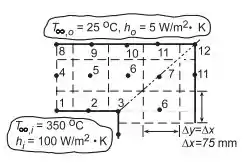
Para obter a taxa de calor, precisamos primeiro determinar as temperaturas Ti. Reconheça que existem quatro tipos de nós: interior (4-7), superfície plana com convecção (1, 2, 8-11), canto interno com convecção (3) e canto externo com convecção (12). Usando as relações apropriadas da Tabela 4.2, as equações de diferenças finitas são
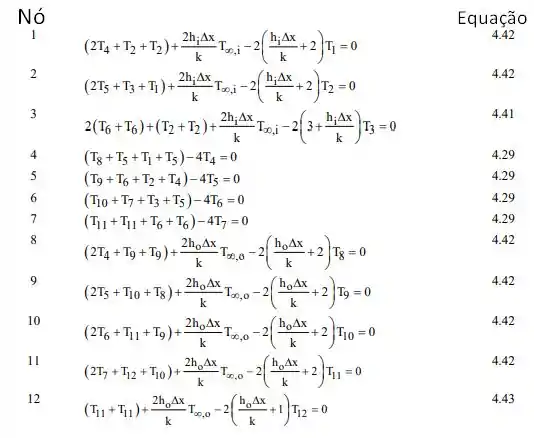
Passo 2
A iteração de Gauss-Seidel é conveniente para este sistema de equações. Seguindo os procedimentos da Seção 4.5.2, o sistema de equações é reescrito na forma apropriada.
As estimativas iniciais (k = 0) são cuidadosamente escolhidas para minimizar o trabalho de cálculo; seja ε
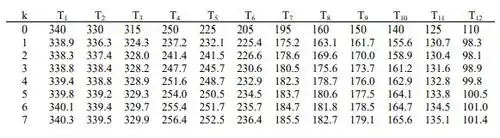
A perda de calor para o ar externo para a superfície superior (nós 8 a 12) é da forma
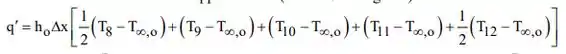
Substituindo:
Assim, para toda a seção transversal da chaminé, considerando a simetria,
