Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 16
Uma placa plana fina de 55 cm por 110 cm está imersa em um fluxo de 6 m/s de óleo SAE 10 a 20oC. Calcule o arrasto total de atrito, caso o fluxo seja paralelo (a) ao lado maior ou (b) ao lado menor.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma placa de imersa em óleo SAE 10 a escoando a , como demonstra o esquema abaixo:
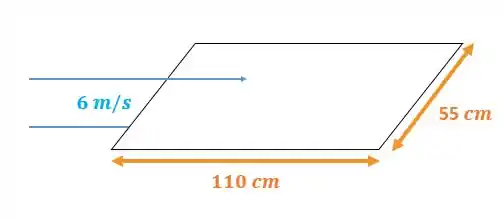
Queremos calcular a força de arrasto para esse escoamento, tanto com o escoamento sendo paralelo ao lado maior (como no esquema acima) e paralelo ao lado menor.
Antes, vamos lembrar qual é a equação para o cálculo da força de arrasto:
Sendo: é o coeficiente de arrasto adimensional, é a massa específica do óleo, a velocidade do escoamento e a soma da área dos dois lados da placa, onde o escoamento acontece.
Nos próximos passos, vamos calcular os e as forças de arrasto para cada uma das situações propostas.
Mas antes da gente começar, vamo lembrar que para óleo SAE 10 a as propriedades físicas são .
Agora sim, vamo resolver essa questão juntos!
Passo 2
Vamos começar resolvendo a letra (a), ou seja, para o escoamento na direção do lado maior com
Em primeiro lugar, temos que calcular o valor do coeficiente de arrasto adimensional.
Antes, no entanto, precisamos saber se o escoamento é laminar ou turbulento, para saber qual equação devemos usar.
Pra isso, vamos calcular o número de Reynolds, onde:
Que está dentro da faixa , ou seja, um escoamento laminar.
Dessa maneira, podemos calcular para o escoamento laminar a partir da equação:
E assim, podemos calcular a força de arrasto:
Passo 3
Pra finalizar a questão, vamo resolver a letra (b), ou seja, para o escoamento na direção do lado maior com
O número de Reynolds é:
Que está dentro da faixa , ou seja, também é um escoamento laminar.
Agora, vamo calcular :
E assim, podemos calcular a força de arrasto:
Pronto, matamos a questão juntos!
Resposta
(a) O arrasto total de atrito para é
(b) O arrasto total de atrito para é