Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 37

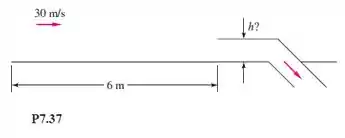
Ar a 20°C e 1 atm escoa sobre uma placa plana longa, em cuja extremidade é colocada uma canaleta estreita, como mostra a Figura P7.37. (a) Calcule a altura h da canaleta para que ela extraia 4 kg/s por metro de largura normal ao papel. (b) Determine o arrasto sobre a placa, até a entrada da canaleta, por metro de largura.

Passo 1

Falaaaa, estamos aqui novamente! Bora resolver essa questãozinha!

Para o ar temos, ρ = 1,2   k g / m 3 e μ = 1,8 × 10 - 5   k g / ( m ⋅ s ) . Bele, queremos calcular a altura quando se extrai 4 kg/s, bora calcular Reynolds pra utilizar nas nossas próximas expressões, temos:

R e x = U x ρ μ = 30 m s 6   m 1,2 k g m 3 1,8 × 10 - 5 k g m ⋅ s = 1,2 × 10 7

Assim,

δ * x ≈ 1 8 0,16 R e x 1 7 = 0,020 1,2 × 10 7 1 7 = 0,00195

Para x = 6   m :

δ * ​ x = 6   m = 6   m 0,00195 = 0,0117   m

Cara, se δ * fosse zero nós teríamos um fluxo uniforme, assim, m ˙ = ρ U h → h 0 = 0,111   m . Porém, temos perdas durante as paredes, assim, a nossa altura será dada por:

h = h 0 + δ * = 0,111   m + 0,0117   m ≈ 0,123   m

Passo 2

Show, bora pra (b)! Assumindo R e t r = 5 E 5 , bora utilizar a Eq. 7.49 para estimar o arrasto, assim:

C a = 0,031 R e x 1 / 7 - 1440 R e x = 0,00302 - 0,00012 = 0,00290

A força de arraste então,

F a r r a s t e = C a ρ 2   V 2 b L = 0,00290 1,2 k g m 3 2 30 m s 2 1   m 6   m = 9,4   N

Resposta

h = 0,123   m

F a r r a s t e = 9,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 9.46, considerando agora que o escoamento de ar é a 10m / s (considere escoamento na camada limite turbulenta).
Para as condições de escoamento do Exemplo 9.4, porém usando o perfil de velocidade de potência 1 / 6 do Problema 9.60, desenvolva uma expressão algébrica para a variação na tensão de cisalhamento de
Para as condições de escoamento do Exemplo 9.4, desenvolva uma expressão algébrica para a variação na tensão de cisalhamento de parede com a distância ao longo da superfície. Integre a fim de obter um
Considere o escoamento de ar sobre uma placa de comprimento L = 5m . Em um gráfico, trace a espessura da camada limite como uma função da distância ao longo da placa para uma velocidade de corrente li
O perfil de velocidade em um escoamento da camada limite com gradiente de pressão zero é aproximado pela expressão de perfil de potência 1 / 6 , u U = η 1 6 , em que η = y δ Use a equação da integral