Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 55
Considere o escoamento de ar sobre uma placa de comprimento Em um gráfico, trace a espessura da camada limite como uma função da distância ao longo da placa para uma velocidade de corrente livre , considerando (a) camada limite laminar em todo o escoamento, (b) camada limite turbulenta em todo o escoamento e (c) uma camada limite que se torna turbulenta em Use o “Resolvedor do Excel(Excel’s Goal Seek and Solver)” para encontrar a velocidade para qual a transição ocorre na borda de fuga e em e .
Passo 1
Precisamos achar para conseguirmos fazer o gráfico, para as seguintes situações:
- camada limite laminar em todo o escoamento, e nessa situação vale que:
- camada limite turbulenta em todo o escoamento, e nessa situação vale que:
- uma camada limite que se torna turbulenta em
E enunciado dá umas informações para gente:
- largura:
- velocidade de corrente livre:
- ar-padrão: e
Vamos começar!
Passo 2
Para o caso (a), podemos dizer que:
Passo 3
Para o caso (b), podemos dizer que:
Passo 4
Para o caso (c):
Nosso muda em:
Passo 5
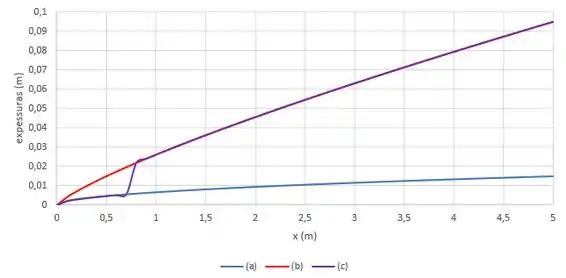
Usando essas expressões e as informações do enunciado, nosso gráfico fica assim:
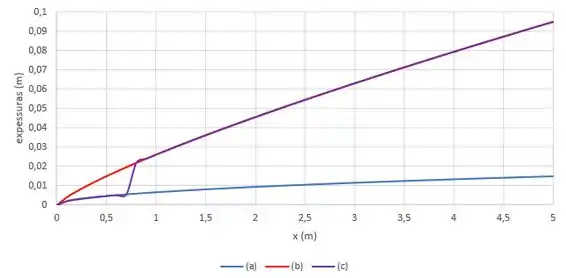
Passo 6
Para usar o “Resolvedor do Excell”, vamos usar essa equação para relacionar e :
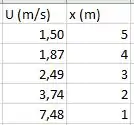
A gente vai colocar como objetivo e como variável a mudar. Fazendo isso, temos esses resultados no Excel:
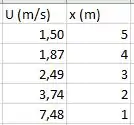
Resposta
