Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 49

Ar a 20°C (1 atm) está escoando sobre uma esfera de diâmetro de 5 cm a uma velocidade de 3,5 m/s. Considerando que a temperatura de superfície da esfera é constante a 80°C, determine (a) o coeficiente de arrasto médio da esfera e (b) a taxa de transferência de calor da esfera.

Passo 1

(a) Vamos usar o gráfico do livro como auxílio para essa aqui, ok?

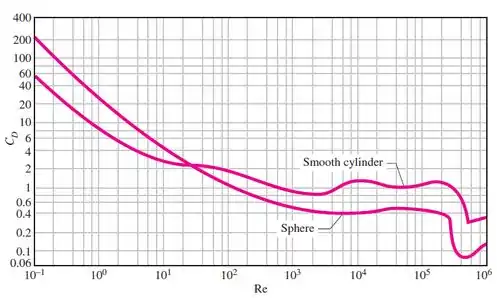
Este é um gráfico de coeficiente de arrasto x Re, ou seja, se você calcular Reynold basta olhar no gráfico a linha da esfera e encontrar o valor de CD (que às vezes também é chamado de Cf)

Vamos tomar as propriedades em Tf, beleza?

K = 0,03 W m . k

v = 1,8   x   10 - 5 m 2 s

P r = 0,72

μ = 1,825   k g / m . s

Passo 2

A primeira etapa que vamos fazer é calcular o Reynold!

R e D = V D v = 3,5   x   0,05 1,8   x   10 - 5 = 9773

E ao olhar no gráfico, você vai encontrar algo próximo de CD = 0,7

Passo 3

(b) Agora é calcular h pela equação de Whitaker para esferas!

N u = h D K = 2 + 0,4 R e 0,5 + 0,06 R e 2 3 P r 0,4   μ μ s 1 4

Onde o subíndice s indica que devemos tomar a propriedade do fluido na temperatura de superfície, nesse caso, µs (T=80°C) = 2,096 x 10-5 kg/m.s

Agora é só substituir os valores das variáveis e calcular que h = 32,57 W m ° C

Passo 4

Agora vamos utilizar nosso balanço de energia

q c o n v = A h T s - T ∞

q c o n v = 4 π r 2 h T s - T ∞ = π D 2 h T s - T ∞

q c o n v = π   x   0,005 2   x   32,57 x   80 - 20 = 15 ,   30   W

Resposta

  1. C D = 0,7
  2. q c o n v = 15,30   W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

69 – Um tanque esférico de 2,2m de diâmetro e espessura desprezível contém água com gelo a 0 ℃ ℃. O ar a 25℃ ℃ escoa sobre o tanque com velocidade de 6m / s . Determine a taxa de transferência de calo
Vento a 30 °C escoa sobre um tanque esférico de 0,5 m de diâmetro contendo água com gelo a 0 °C, a uma velocidade de 25 km/h. Se o reservatório é de casca fina com material de alta condutividade térmi
Uma pequena esfera de chumbo de 3,0 mm de diâmetro é resfriada da temperatura média de 200 °C para 54 °C, sendo largada em uma coluna alta preenchida com ar a 27 °C e 101,3 kPa. Pode-se supor que a ve
Repita o Prob. 7-107 para uma esfera de 5 mm de diâmetro.
Ar ambiente a 20 °C escoa sobre um objeto esférico quente de 30 cm de diâmetro a uma velocidade de 4,2 m/s. Considerando que a temperatura média da superfície do objeto é 200 °C, o coeficiente médio d