Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 31
Considere um caminhão de refrigeração viajando a 110 km/h em um localonde a temperatura do ar é de 25°C. O comportimento frigorífico do caminhão pode ser considerado como uma caixa retangular de 2,8 m de largura, 2,1 m de altura e 6 m de comprimento. O sistema de refrigeração do caminhão pode fornecer 3 toneladas de refrigeração (ou seja, pode remover o calor a uma taxa de 633 KJ/min). A superfície externa do caminhão é revestida com material de baixa emissividade, e, assim, a transferência de calor de radiação é muito pequena. Determine a temperatura média da superfície externa do compartimento de refrigeração do caminhão se o sistema de refrigeração operar com metade da capacidade. Suponha que o fluxo de ar sobre a superfície externa interna é turbulento e o coeficiente de transferência de calor nas superfícies dianteira e traseira é igual ao das superfícies.
Passo 1
Vamos olhar pra superfície do compartimento, beleza?
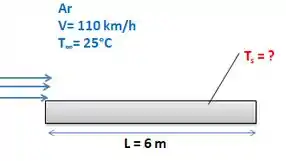
Precisamos chutar uma temperatura Ts para obtermos as propriedades em Tf, e, eu vou chutar 35°C, então e as propriedades do ar nessa temperatura são:
E lembra de sempre ter tudo no SI, então, vamos passar essa velocidade para m/s
Além disso, percebe que o enunciado nos deu o valor de q, porém em outra unidade, KJ/min e vamos passar isso pra J/s = W, beleza?
E o problema quer que encontremos a temperatura Ts e, como foi dito, não rola radiação, então o calor perdido por ar ambiente só pode ser por convecção, sacou?
E essa é a nossa equação principal!! Agora vamos encontrar o parâmetro que tá falando pra calcular Ts, que é o h.
Passo 2
Vamos calcular como sempre, primeiro, o valor de Reynold!
Estamos acima do valor crítico, então consideremos um regime combinado.
Passo 3
Agora é só encontrar a correlação adequada as condições de Ts constante, placa plana e regime combinado e você vai ver que a melhor é essa aqui ó:
Agora é só substituir os valores e ser feliz ;)
Passo 4
Já descobrimos o carinha que estava nos atrapalhando a encontrar Ts, então é só pegar a equação principal lá do passo 1 e resolver para termos o valor desejado!! Viu como Transcal é LINDAAAAAAA
Como você já deve ter visto em outras questões, idealmente esse tipo de problema é iterativo e você teria que ficar fazendo iterações até que a Ts encontrada fosse a mesma usada para estimar Tf