Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 32
32 - No Capítulo 3, supusemos que, sempre que aletas eram fixadas a uma superfície (base), a temperatura da base permanecia inalterada. O que ocorre na realidade, se a temperatura da base for superior à temperatura do fluido, é que a fixação de uma aleta reduz a temperatura na junção a um nível inferior ao valor da temperatura original da base e o fluxo de calor do material da base para a aleta é bidimensional.
Considere condições nas quais um longo pino de alumínio, com diâmetro , é fixado a um material base cuja temperatura em um ponto distante da junção é mantida a . As condições de convecção no pino correspondem a e .
(a) Quais são a taxa de transferência de calor no pino e a temperatura na junção, quando o material da base for (i) alumínio e (ii) aço inoxidável ?
(b) Repita os cálculos anteriores supondo haver uma resistência térmica de contato de associada ao método utilizado para a fixação do pino ao material base.
(c) Considerando a resistência térmica de contato, para cada um dos dois materiais, represente graficamente a taxa de transferência de calor no pino em função do coeficiente convectivo, na faixa de
Passo 1
Segue o desenho do circuito térmico para as aletas.
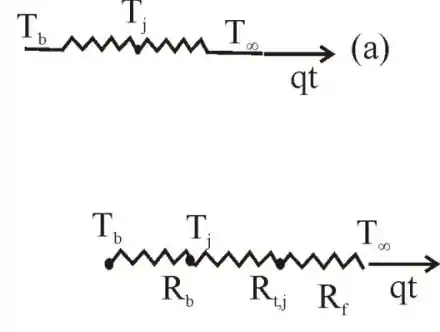
Passo 2
a)
Para alumínio:
Obtenha o fator de forma na "Tabela 4.1 fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados" no manual para disco de diâmetro e temperatura em um meio semi-infinito de condutividade térmica (o pino é considerado como disco).
Encontre a resistência da base.
Aqui, é o diâmetro da aleta, é a condutividade térmica do material de base.
Passo 3
Vamos agora encontrar o perímetro da aleta.
Agora, encontre a área da seção transversal da aleta.
Passo 4
Encontre a resistência da aleta.
Aqui é o coeficiente de transferência de calor por convecção.
Escreva a expressão para taxa de calor.
Aqui, é a temperatura base e é a temperatura da superfície.
Portanto, a taxa de calor da aleta é .
Passo 5
Encontre a temperatura da junção.
Portanto, a temperatura da junção é .
Passo 6
Agora vamos para o aço inoxidável.
Encontre a resistência da base.
Passo 7
Encontre a taxa de calor.
Aqui, é a temperatura base e é a temperatura da superfície.
Portanto, a taxa de calor da aleta é .
Agora, vamos encontrar a temperatura da junção.
Portanto, a temperatura da junção é .
Passo 8
b)
Considere a resistência de contato térmico.
Encontre a resistência térmica.
Para alumínio
Encontre a taxa de transferência de calor.
Portanto, a taxa de calor da aleta é .
Passo 9
Encontre a temperatura da junção.
Portanto, a temperatura da junção é .
Passo 10
Para o aço.
Encontre a taxa de transferência de calor.
Portanto, a taxa de calor da aleta é .
Passo 11
Encontre a temperatura da junção.
Portanto, a temperatura da junção é .
Passo 12
c) Encontre a taxa de transferência de calor.
Passo 13
Tabule os valores de transferência de calor variando o coeficiente de transferência de calor para o alumínio.
Passo 14
Encontre a taxa de transferência de calor para o aço inoxidável agora.
Passo 15
Tabule os valores de transferência de calor variando o coeficiente de transferência de calor para o aço inoxidável.
Passo 16
Plote o gráfico entre o coeficiente de transferência de calor e a taxa de transferência de calor.
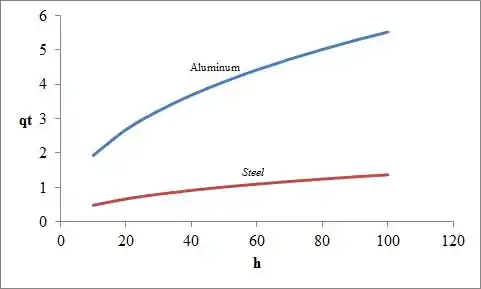
Resposta
- Para o alumínio: e .
- Para o alumínio: e .
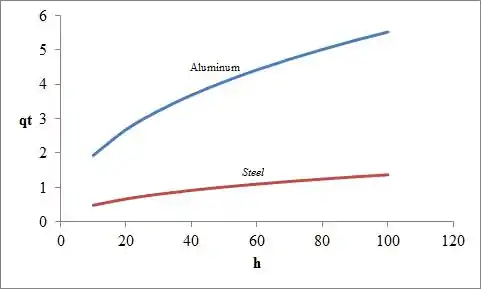
Para o aço inoxidável: e
Para o aço inoxidável: e