Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 112
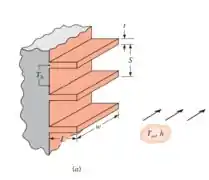
Devido ao bloqueio do fluxo de fluido, a taxa de transferência de calor, para as superfícies aletadas com uma série de aletas, normalmente decresce com o aumento do número de aletas. Considere, a série de aletas mostradas na figura 3.21ª, com uma parede com uma altura de , , e . As aletas são de alumínio e a base está a uma temperatura de , enquanto o ambiente está a uma temperatura de . Como uma primeira aproximação, assuma que, onde é o máximo número de aletas que podem ser colocadas na superfície, então . Para , determine a taxa total de transferência de calor para, aletas.
Passo 1
Olá jovem, bora de mais uma questãozinha de aleta?? Simbora!
Seguinte, exercício sem muito segredos. Basta aplicarmos as fórmulas das nossas aletas.
Lembrando que, para uma superfície aletada:
Onde:
E
Lembrando ainda, que para aletas quadradas como a nossa.
Bom, vamos começar achando o nosso , você pode achar ele na tabela . Vamos assumir que ele seja mais ou menos: .
E então podemos começar a calcular.
Passo 2
- Zero aletas.
- Para 3 aletas.
- Para 6 aletas:
- Para 9 aletas:
A nossa expressão para a taxa de transferência se reduz à:
Com,
Teremos então,
E então:
A nossa fórmula volta a ser:
Dessa vez,
e
Lembrando que levamos em conta as áreas de cima e de baixo de uma única aleta (podemos desconsiderar que exista fluxo pela espessura da aleta). Mas como temos 3 aletas:
Com isso, a área exposta da parede é reduzida:
E sem esquecer da eficiência da aleta:
Com,
Então:
Finalmente:
Passo 3
Tá comigo?? Tamo quase! Força Pikachu!
Com,
As nossas áreas serão:
E
Teremos ainda:
E portanto:
E então:
Teremos:
E
E então:
Ou seja:
UFaaa! Então é isso. Até a próxima jovem!!
Resposta
Portanto:
- Sem aletas:
- 3 aletas:
- 6 aletas:
- 9 aletas: