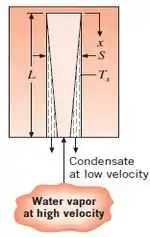
40 – Taxas de condensação podem ser restritas pela velocidade do som na fase vapor. Consequentemente, a condensação pode se aproximar de um limite sônico. Considere uma rachadura de S= 2 mm de largura e L= 200mm em um bloco sólido de metal. A rachadura é longa, então o escoamento do fluido é bidimensional. Vapor de água saturada a pressão atmosférica condensa nas duas superfícies longas verticais da rachadura, na qual são mantidas a Ts=40°C. Com o decorrer da condensação, água liquida sai da rachadura através da abertura no fundo e é reabastecido por vapor de água saturada escoando para cima através da mesma abertura. Estime o nº de Mach do vapor de água escoando para cima através da abertura. Em qual largura da rachadura o nº de Mach do vapor de água alcança a unidade?

Buscando na literatura uma relação matemática para o nº de Mach e as propriedades termodinâmicas, tem-se que, uma expressão modelada com base nas equações de balanço de massa e balanço de quantidade de movimento, aplicada para uma diferença de temperatura em função do número de Mach que varia em função de x, essa expressão é dada por:

Onde, γ é a razão de calores específicos e x aqui é a largura L.

A razão de calores específicos é dada por:

Onde,

Onde, R é a constante dos gases ideais.

Vamos tentar isolar o nº de Mach da Eq.1:

Fazendo, para simplificar

Vamos pegar os dados termodinâmicos necessários.

A temperatura de saturação da água na pressão atmosférica é:

A temperatura da superfície na unidade de kelvin é:

Pela literatura, a razão de calores específicos para o vapor de água pode ser estimada com um valor aproximado de:

Vamos aos cálculos.

Calculando z:

Substituindo os valores na Eq2:

Fazendo

Vamos ter que

Chegamos em uma equação do segundo grau que podemos resolver por Bhaskara.

Assim,

Para determinarmos a largura pela a qual o número de Mach é unitário, podemos simplesmente usar a Eq1 e isolar L. Fazendo isso:

Para Ma = 1: