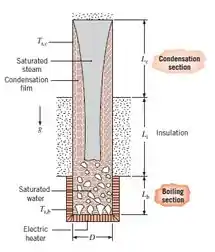
56 – Considere o termossifão do Problema 10.54. Em muitas aplicações, um cenário mais realístico é onde, na seção de condensação, um fluido externo escoando é usado para resfriar. Determine a taxa de transferência de calor do termossifão bem como as temperaturas da superfície das seções de ebulição, Ts,b, e condensação, Ts,c, se a superfície cilíndrica vertical da seção de condensação é exposta a um fluido a 20ºC e coeficiente de transferência de calor por convecção de 500 W/m2K. Dica: Você pode querer começar assumindo que a resistência térmica externa é dominante na seção de condensação para estimar o fluxo de calor.

Vamos agora relacionar esse fluxo de calor com a taxa de transferência de calor no termossifão. A taxa de transferência de calor, q, do termossifão será o fluxo de calor vezes a área de superficial total da seção de ebulição, visto que o calor transferido da seção de ebulição deve ser igual ao calor removido da seção de condensação. Assim,

A área da seção de ebulição, AS,b, é dada por

Logo,

Pegando os dados do problema 10.54:

Aplicando os valores

Vamos agora determinar as temperaturas nas superfícies:

Para a temperatura da superfície da seção de ebulição, Ts,b, podemos usar a equação de Rohsenow desenvolvida para processos ebulição nucleada, cuja expressão é

Onde,

-q” é o fluxo de calor entre a superfície do material e o fluido;

-μl, ρl, cp,l e σ são, respectivamente, a viscosidade dinâmica, a densidade, o calor especifico e a tensão superficial do liquido saturado;

-ρv é a densidade do vapor;

-Hvap é a entalpia de vaporização do fluido;

-Prl é o nº de Prandtl do liquido saturado;

-g é a constante da gravidade, 9,81 m/s2;

-TS,b e Tsat são, respectivamente, a temperatura da superfície do material e a temperatura de saturação do fluido;

-Cs,f e n são constantes que dependem da combinação do material sólido com o fluido, e são encontrados em tabela.

Vamos tentar isolar Ts,b

Pelo problema 10.54:

O fluxo é determinado por uma expressão que já vimos antes

Calculando TS,b:

Agora a temperatura na superfície da seção de condensação, TS,C:

Na seção de condensação, que consiste em uma placa que compõem o sistema do chip em contato com o tubo cilíndrico, ocorre uma transferência de calor por convecção, assim

Onde,

-q é a taxa de transferência de calor do termossifão;

-qconv é a taxa de transferência de calor por convecção;

-hS,C é coeficiente de transferência de calor na seção de convecção, hS,C=h=500W/m2K;

-AS,C é a área superficial do tubo na seção de convecção;

A área AS,C é dada pela área superficial de um cilindro com as dimensões da seção de condensação:

Assim,

Isolando TS,C

Pegando os dados do problema 10.54:

Aplicando os valores: