Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 2

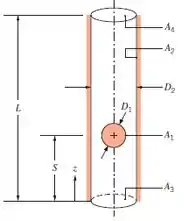
2 – Uma partícula esférica de raio r1= 5 mm está suspensa por um fio fino dentro de um tubo cilíndrico de raio interno r2 = 15 mm e comprimento L = 0,5 m. Determine os fatores de forma F11, F12, F13 e F14 para S = 5 e 250 mm. O fator de forma entre a esfera e o fundo do tudo (um disco de raio r3) é

F 13 = 0,5 1 - 1 + R 3 2 - 1 2

Onde,

R 3 = r 3 S

Passo 1

Para este exercício, você terá que trabalhar com as expressões matemáticas vistas no capítulo relativas aos fatores de forma.

Ao longo da resolução vamos relembrar quais são elas.

Passo 2

Teremos então que determinar expressões para cada fator de forma. Já temos para o fator de forma F13 e também podemos encontrar o fator F11 a partir de conceitos.

Pela regra da soma temos que para F11 será zero, pois se trata de uma superfície convexa e para superfícies convexas todo fator de forma do tipo Fii é nulo, assim

F 11 = 0

Passo 3

Podemos determinar o fator de forma F12 usando a eq. 13.1 do Incropera, que é:

F i j = 1 A i ∬ cos ⁡ ( θ i ) cos ⁡ ( θ j ) π R 2 d A i d A j

Onde, i = 1 e j = 2.

Vamos considerar que os ângulos θ e o raio R são independentes da posição de Ai, assim

F i j = ∫ cos ⁡ ( θ i ) cos ⁡ ( θ j ) π R 2 d A j

Considerando os ângulos iguais

θ i = θ j = θ

Assim,

F i j = ∫ cos 2 ⁡ ( θ ) π R 2 d A j

Como se trata de um cilindro então podemos fazer as seguintes relações:

R 2 = r 2 + L 2 ;   d A j = 2 π r d r ; cos ⁡ ( θ ) = L R

Assim,

F 12 = ∫ 0 r 2 L 2 / R 2 π R 2 2 π r d r

F 12 = ∫ 0 r 2 L 2 π R 4 2 π r d r

F 12 = 2 L 2 ∫ 0 r 2 r r 2 + L 2 2 d r

Resolvendo a integral acima vamos chegar que:

F 12 = r 2 2 r 2 2 + L 2

Passo 4

Já temos uma expressão para o fator de forma F13:

F 13 = 0,5 1 - 1 + R 3 2 - 1 2

F 13 = 0,5 1 - 1 + r 3 S 2 - 1 2

E para acharmos o fator de forma F14 podemos usar a equação da regra do somatório:

∑ j F i j = 1

Assim,

F 11 + F 12 + F 13 + F 14 = 1

Como F11 = 0 e isolando F14:

F 14 = 1 - F 12 + F 13

Assim,

F 14 = 1 - r 2 2 r 2 2 + L 2 - 0,5 1 - 1 + R 3 2 - 1 2

Passo 5

Já temos as expressões para todos os fatores de forma, agora basta aplicarmos os valores:

Para S = 5 mm:

F 12 = 15 m m 2 15 m m 2 + ( 500 m m ) 2 = 0,0009

F 13 = 0,5 1 - 1 + 15 m m 5 m m 2 - 1 2 = 0,342

F 14 = 1 - 0,0009 - 0,342 = 0,6572

Para S = 250 mm:

F 12 = 15 m m 2 15 m m 2 + ( 500 m m ) 2 = 0,0009

F 13 = 0,5 1 - 1 + 15 m m 250 m m 2 - 1 2 = 0,0009

F 14 = 1 - 0,0009 - 0,0009 = 0,9982

Resposta

Para S = 5 mm:

F 12 = 0,000 9

F 13 = 0,34 2

F 14 = 0,657 2

Para S = 250 mm:

F 12 = 0,000 9

F 13 = 0,000 9

F 14 = 0,998 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura ( d ) e dimensão principal ( L ) , como mostrado na figura.(a) Determine o fator de forma entr
Um forno cúbico, com 2m de lado, é usado para tratar termicamente uma placa de aço. A superfície superior do forno é formada por aquecedores elétricos radiantes que têm uma emissividade de 0,85 e são
Silício sólido puro é produzido a partir de material fundido, como por exemplo, no Problema 1.37. Silício sólido é semitransparente e a distribuição do coeficiente de absorção espectral para o silício
Considere um forno circular que tem 0,5m de comprimento e 0,5m de diâmetro. As duas extremidades têm superfícies cinzas e difusas, que são mantidas a 400 e 500K , com emissividades de 0,4 e 0,5 , resp
Um forno que tem uma cavidade esférica com 0,4m de diâmetro contém uma mistura gasosa a 1a t m e 1400K . A mistura é formada por C O 2 , com uma pressão parcial de 0,25a t m , e nitrogênio com uma pre