Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 47

47. Uma lâmina plana unidimensional, com propriedades constantes, com espessura 2L e inicialmente a uma temperatura uniforme, é aquecida convectivamente com Bi = 1.

(a) Em um tempo adimensional de Fo1, o aquecimento é subitamente interrompido e a lâmina é rapidamente coberta com um isolante. Esboce as temperaturas adimensionais da lâmina no plano central e na superfície como uma função do tempo adimensional na faixa 0

(b) Fazendo Fo2 = Fo1 + ΔFo, deduza uma expressa analítica para ΔFo e avalie ΔFo para as condições da parte (a).

(c) Determine ΔFo para Bi = 0,01; 0,1; 10; 100; e ∞, quando tanto Fo1 quanto Fo2 são maiores do que 0,2.

Passo 1

Letra (a)

Em, a superfície da laje estará quente em relação ao plano médio, uma vez que os gradientes de temperatura na laje são significativos. No corte do aquecimento, a temperatura da superfície esfria rapidamente, enquanto as temperaturas quentes continuam a se propagar em direção ao plano intermediário, aquecendo lentamente o plano intermediário até que uma condição isotérmica no estado estacionário seja finalmente alcançada.

Pode-se alcançar uma temperatura no plano intermediário no estado estacionário igual à temperatura no plano intermediário  F 01 , reduzindo a duração do aquecimento convectivo para  F 02 , conforme mostrado na figura 2:

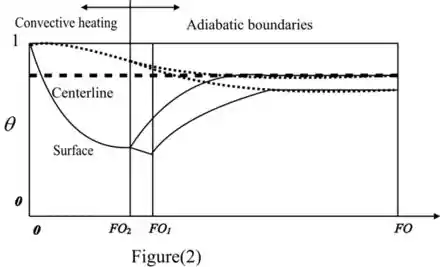
Na figura (2), o valor  F 0 1 é maior que o valor   F 0 2

Portanto  F 0 2 < F 0 1 .

Passo 2

Letra (b)

Observando que a temperatura no estado estacionário da laje é uniforme e relacionada à energia transferida para a laje.

A energia total transferida das superfícies isotérmicas de um plano e a energia total transferida para o interior da parede do avião são relacionadas da seguinte forma:

θ 0 * F 01 = 1 - Q Q 0 F 02

θ 0 * F 01 = 1 - Q Q 0 F 0 1 + ∆ F 0     ( 1 )

A temperatura da linha central e o número de Fourier são relacionados pela seguinte fórmula:

θ 0 * = C 1 exp ⁡ - ξ 1 2 F 01     ( 2 )

A energia total transferida das superfícies isotérmicas de um plano e a energia total transferida para o interior da parede do avião são relacionadas da seguinte forma:

Q Q 0 = 1 - sin ⁡ ξ 1 ξ 1 θ 0 '

Para calcular a variação do número de Fourier substituto  C 1 exp ⁡ - ξ 1 2 F 01     para  θ 0 *   e  1 - sin ⁡ ξ 1 ξ 1 θ 0 '   por  Q Q 0 na equação (1):

1 - C 1 exp ⁡ - ξ 1 2 F 01 = 1 - sin ⁡ ξ 1 ξ 1 θ 0 ' exp ⁡ - ξ 1 2 F 01 + Δ F 0

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Se o número Biot, B i = 1 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 0,8603 r a d 2 ln ⁡ 0,8603 r a d sin ⁡ 0,8603 r a d × 57,29

= - 0,1709

Assim, o  Δ F 0 valor em  B i = 1   é - 0,1709  .

Passo 3

Letra (c)

Se o número Biot, B i = 0,01 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 0,0998 r a d 2 ln ⁡ 0,0998 r a d sin ⁡ 0,0998 r a d × 57,29

= - 0,1667

Assim, o  Δ F 0 valor em  B i = 0,01   é - 0,1667  .

Se o número Biot, B i = 0 , 1 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 0,3111 r a d 2 ln ⁡ 0,3111 r a d sin ⁡ 0,3111 r a d × 57,29

= - 0,1672

Assim, o  Δ F 0 valor em  B i = 0 , 1   é - 0,1672  .

Se o número Biot, B i = 1 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 0,8063 r a d 2 ln ⁡ 0,8063 r a d sin ⁡ 0,8063 r a d × 57,29

= - 0,1709

Assim, o  Δ F 0 valor em  B i = 1   é - 0,1709  .

Se o número Biot, B i = 1 0 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 1,4289 r a d 2 ln ⁡ 1,4289 r a d sin ⁡ 1,4289 r a d × 57,29

= - 0,1847

Assim, o  Δ F 0 valor em  B i = 1 0   é - 0,1847  .

Se o número Biot, B i = 10 0 .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 1,552 r a d 2 ln ⁡ 1,552 r a d sin ⁡ 1,552 r a d × 57,29

= - 0,1826

Assim, o  Δ F 0 valor em  B i = 1 00   é - 0,1826  .

Se o número Biot, B i = ∞ .

O  Δ F 0 valor pode ser calculado pela seguinte fórmula:

Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1

Δ F 0 = - 1 1,5708 r a d 2 ln ⁡ 1,5708 r a d sin ⁡ 1,5708 r a d × 57,29

= - 0,1830

Assim, o  Δ F 0 valor em  B i = ∞   é - 0,1830  .

Resposta

  1. F 0 2 < F 0 1
  2. Δ F 0 = - 1 ξ 1 2 ln ⁡ ξ 1 sin ⁡ ξ 1 e o  Δ F 0 valor em  B i = 1   é - 0,1709  .
  3. B i = 0,01   é - 0,1667 / B i = 0,1   é - 0,1672  / B i = 1   é - 0,1709   / B i = 10   é - 0,1847  / B i = 100   é - 0,1826  / B i = ∞   é - 0,1830
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Seção 5.2 observamos que o valor do número de Biot influencia de forma significativa a natureza da distribuição de temperaturas em um sólido durante um processo condutivo transiente. Reforce o seu
No tratamento térmico para endurecer bilhas de rolamento feitas em aço ( c=500J / ( k g·K ) ,ρ=7800k g / m 3 ,k=50W / ( m·K ) ) , é desejável aumentar a temperatura superficial por um curto período de
Uma câmara de ar frio é proposta para o resfriamento de esferas de aço com diâmetro D=0,2m e temperatura inicial Ti = 400°C. O ar na câmara é mantido a −15°C por um sistema de refrigeração e as esfera
Uma esfera com 30 mm de diâmetro inicialmente a 800 K é resfriada em um grande banho, mantido a uma temperatura constante de 320 K e com um coeficiente de transferência de calor por convecção de 75 W/
Para determinar quais partes do cérebro de uma aranha são ativadas com atividade neural em resposta a vários estímulos óticos, os pesquisadores na Universidade de Massachusetts – Amherst desejam exami