Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 48
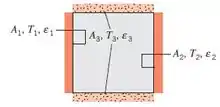
48 – Um longo condute é construído com paredes amplas cinzas e difusivas de 0,5 m. O topo e o fundo do condute está isolado. As emissividades das paredes são ε1 = 0,45, ε2 = 0,65 e ε3 = 0,15, respectivamente, enquanto que as temperaturas das paredes 1 e 2 são 500 K e 700 K, respectivamente.
A) Determine a temperatura da parede isolada.
B) Determine a taxa de transferência de calor liquida por radiação da superfície 2 por unidade de comprimento do condute.
Passo 1
Para este problema vamos considerar que temos três placas paralelas, a parede 1 paralela à parede 3, e a parede 3, paralela à parede 2.
Com isso, vamos usar as equações para o fluxo de calor associado a essas características.
Passo 2
O fluxo de calor para duas placas planas paralelas pode ser calculado pela Eq. 13.24, que é:
Esse é o fluxo de calor envolvendo as paredes 1 e 3.
Onde, σ é a constante de Stefan-Boltzmann:
Para as paredes 2 e 3 temos que:
Passo 3
Considerando fluxo de calor constante pelo condute, assim vamos ter que:
Vamos tentar isolar T3:
Fazendo
Passo 4
Aplicando os valores
Passo 5
B)
Para a superfície 2 temos que:
Em termos de taxa por unidade comprimento:
Aplicando os valores:
Resposta
A)
B)