Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 37
Quando uma lâmina de aço deixa a última série de rolos em um processo de laminação a quente, antes de ser bobinada, ela é temperada com a utilização de jatos planos de água. Devido às elevadas temperaturas na lâmina, ocorre ebulição em filme na região logo após a colisão do jato.
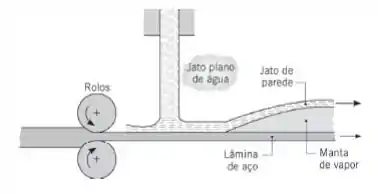
Considere condições nas quais a lâmina de aço abaixo da manta de vapor está a uma temperatura de 907 K e tem uma emissividade de 0,35. Desprezando os efeitos dos movimentos da lâmina e do jato, e supondo que a ebulição no filme possa ser aproximada por aquela associada a um grande cilindro horizontal com 1 m de diâmetro, estime a taxa de transferência de calor, por unidade de área superficial, da lâmina para o jato de parede.
Passo 1
Partiu resolver essa questãozinha aí! Nosso enunciado quer a taxa de transferência de calor, beleza?
Para isso vamos precisar de dados adicionais… Fica frio! É só a gente visitar o anexo do livro, lá na tabela A-6, com uma temperatura de :
E na tabela A-4, com :
Beleza agora pode achar o que ele quer!
Passo 2
A taxa de transferência de calor nós podemos encontrar assim, olha só:
Mas pra chegar aí temos que encontrar algumas coisas antes:
Vamos começar com o , certo?
Esse podemos achar assim:
Não se assusta não, ok? Vamos encontrar primeiro esse :
Vamos voltar na equação anterior:
Nosso coeficiente de convecção será:
Passo 3
Agora vamos achar o coeficiente de radiação, belezinha?
Show! Podemos partir para aquelas equações lá do começo do passo 2, vamos nessa!
E para fechar com chave de ouro vamos ter:
Uhull!! Conseguimosss!