78 - Um elemento aquecedor elétrico fino fornece um fluxo térmico uniforme para a superfície externa de um duto através do qual escoa ar. A parede do duto tem uma espessura de e uma condutividade térmica de .

(a) Em uma determinada posição, a temperatura do ar é de e o coeficiente de transferência de calor por convecção entre o ar e a superfície interna do duto é de . Qual é o fluxo térmico necessário para manter a superfície interna do duto a ?

(b) Para as condições da parte (a), qual é a temperatura da superfície do duto próxima ao aquecedor?

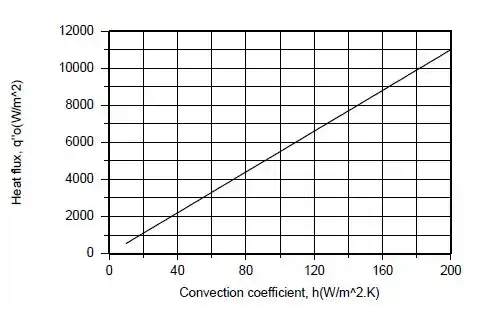
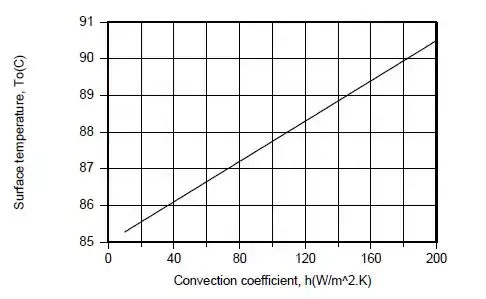
(c) Com , calcule e represente graficamente e como funções do coeficiente de transferência de calor por convecção h no lado do ar, na faixa . Discuta de modo resumido os seus resultados.

b) Considerando a Lei de Fourier’s e a parede do tubo, temos:

Para , os resultados desejados podem ser obtidos através da resolução simultânea das equações do balanço energético.

e

Após ter calculado, temos os seguintes gráficos feito pelo computador.

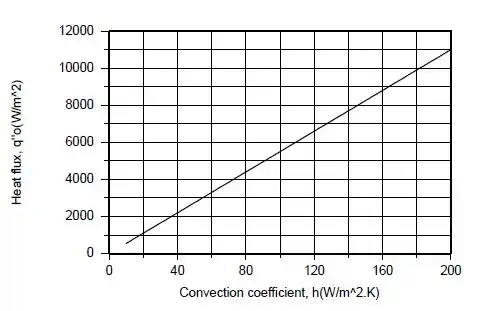
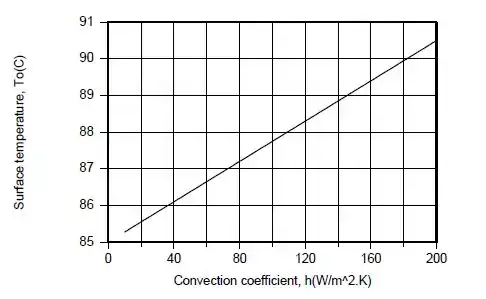
Como aumenta linearmente com o aumento de , o fluxo de calor aplicado e também deve aumentar. Um aumento em, que, com fixo, e , requer um aumento em .

COMENTÁRIOS: A diferença de temperatura na parede é pequena, atingindo um valor máximo de para . Se a parede fosse mais fina ou feita de um material com maior condutividade , essa diferença seria reduzida.