Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 91
Se no escoamento com simetria axial é definida pela equação 8.85 e as coordenadas são dadas na figura 8.29, determine qual a equação diferencial parcial que deve satisfazer.
Passo 1
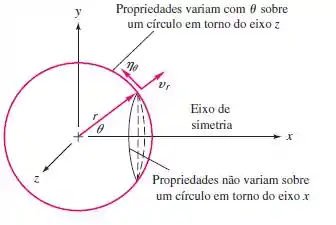
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é vamos olhar a figura 8.29 que é indicada no enunciado!
Passo 2
As velocidades são relatadas em pela equação 8.87 do livro e uma substituição direta nos dará que:
Com e também
Passo 3
Ao final, nossa EDP ficará na seguinte forma em função de e
Resposta
Exercícios de Livros Relacionados
The vertical keel of a sailboat approximates a Rankine oval125 cm long and 30 cm thick. The boat sails in seawater instandard atmosphere at 14 knots, parallel to the keel. At asection 2 m below the su
Modify Prob. P8.52 as follows. For the same sailboat data,find the wind velocity, in mi/h, that will drive the boat at anoptimum speed of 8 kn parallel to its keel.
At point A in Fig. P8.21 is a clockwise line vortex ofstrength K 5 12 m2/s. At point B is a line source of strengthm 5 25 m2/s. Determine the resultant velocity induced bythese two at point C.
The original Flettner rotor ship was approximately 100 ftlong, displaced 800 tons, and had a wetted area of 3500 ft2. Assketched in Fig. P8.54, it had two rotors 50 ft high and 9 ft indiameter rotatin
Line sources m1 and m2 are near point A, as in Fig. P8.32.If m1 5 30 m2/2, fi nd the value of m2 for which the resultantvelocity at point A is exactly vertical