Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 32
Line sources m1 and m2 are near point A, as in Fig. P8.32.
If m1 5 30 m2/2, fi nd the value of m2 for which the resultant
velocity at point A is exactly vertical
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Desenhando o diagrama
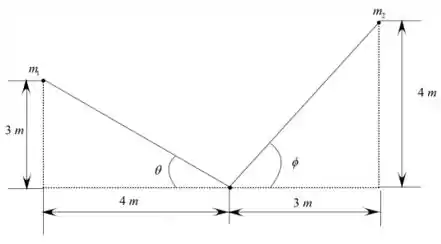
Passo 2
Resolva as forças de aceleração horizontalmente.
Aqui, é a aceleração do lado esquerdo, é a aceleração do lado direito, é o ângulo feito pela aceleração do lado esquerdo, e é o ângulo feito pela aceleração do lado direitoCalcule o valor de .
Passo 3
Calcule o valor de .
Substituindo valores na equação (1)
Assim, o valor de é .
Resposta
Exercícios de Livros Relacionados
A uniform stream, U∞ 5 4 m/s, approaches a Rankine ovalas in Fig. 8.13, with a 5 50 cm. Find the strength m of thesource–sink pair, in m2/s, which will cause the total lengthof the oval to be 250 cm.
The Transition® car-plane in Fig. 7.30 has a gross weight of1430 lbf. Suppose we replace the wing with a 1-ft-diameterrotating cylinder 20 ft long. (a) What rotation rate fromFig. 8.15, in r/min, woul
The Flettner rotor sailboat in Fig. E8.3 has a water dragcoefficient of 0.006 based on a wetted area of 45 ft2. If therotor spins at 220 r/min, fi nd the maximum boat velocitythat can be achieved in a
Hurricane Sandy, which hit the New Jersey coast on Oct.29, 2012, was extremely broad, with wind velocities of40 mi/h at 400 miles from its center. Its maximum velocitywas 90 mi/h. Using the model of F
Consider potential fl ow of a uniform stream in the x direction plus two equal sources, one at (x, y) 5 (0, 1a) and theother at (x, y) 5 (0, 2a). Sketch your ideas of the bodycontours that would arise