Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 21

At point A in Fig. P8.21 is a clockwise line vortex of

strength K 5 12 m2/s. At point B is a line source of strength

m 5 25 m2/s. Determine the resultant velocity induced by

these two at point C.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

A figura que representa o sistema de forças:

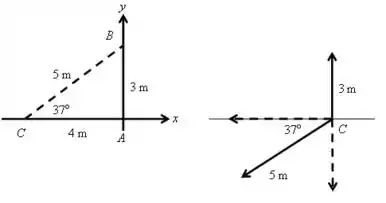
Passo 2

A velocidade no ponto C devido à força em A é,

V C / A = K r A C

Substitua r A C = 4   m e K = 12   m 2 / s na equação acima.

V C / A   = 12 4   = 3   m / s

A velocidade no ponto C devido à força em B é,

V C / B = m r B C

Aqui

r B C   = r A C 2 + r A B 2   = 4 2 + 3 2   = 5   m

Assim

V C / B   = 25 5   = 5   m / s

Passo 3

O ângulo feito por V C / B com a horizontal é,

θ   = t a n - 1 ⁡ 3 4   = 37 ∘

Agora, o componente de velocidade ao longo x da direção da Figura é,

∑   u   = - 5 c o s ⁡ 37 ∘   = - 3.99   m / s

O componente de velocidade ao longo y da direção da Figura é,

∑   v   = 3 - 5 s i n ⁡ 37 ∘   = - 0.009   m / s

Assim, a velocidade resultante é,

V   = u 2 + v 2   = 3.99 2 + 0.009 2   = 3.99   m / s

Portanto, a velocidade resultante induzida no ponto C é 3.99   m / s .

Resposta

V = 3.99   m / s

Exercícios de Livros Relacionados

PP8.2 – Modifique o Problema PP8.1 para determinar a distribuição de fontes pontuais que aproxima um corpo de revolução de formato “0018”. Uma vez que não existe resultados publicados, simplesmente se
An incompressible, irrotational, two-dimensional fl ow hasthe following stream function in polar coordinates:ψ 5 A rn sin (nθ) where A and n are constants.Find an expression for the velocity potential
Consider the function f 5 ay 2 by3. (a) Could this represent a realistic velocity potential? Extra credit: (b) Could itrepresent a stream function?
The proposed fl ow in Prob. P4.19 does indeed satisfy theequation of continuity. Determine the polar-coordinatestream function of this flow.
An incompressible stream function is given byψ 5 aθ 1 br sin θ. (a) Does this fl ow have a velocitypotential? (b) If so, find it.