86 – A usina hidrelétrica Tupperware no rio Blackstone tem quatro turbinas de 914 mm de diâmetro, cada uma produzindo 447 kW a 200 rpm com 5,8 m3/s para uma altura de queda de 9,1 m. De que tipo são essas turbinas? Como seus desempenhos se comparam com os da Figura

11.22?

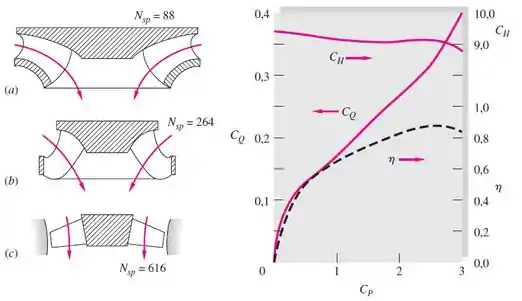
Figura 11.22: (a) Turbina Francis do tipo radial; (b) Turbina Francis de fluxo misto;

(c) Turbina hélice, de fluxo axial;

À direita na figura temos as curvas de desempenho de uma Turbina Francis, n=600rpm, D=0,7m e Nsp=127.

Agora vamos calcular a rotação especifica para vermos qual é o tipo de turbina. A expressão para Nsp é

Onde,

-n é a rotação, em rpm;

-Nsp é a rotação especifica da turbina;

-Pe é a potência de eixo de saída de cada turbina;

-H é a altura de queda.

Para o cálculo da rotação especifica as unidades para cada variável deve ser as seguintes

Assim, convertendo a potência individual de cada turbina para unidades de hp.

Aplicando os valores

Agora com esse valor, vamos até a tabela disponível no livro do White, Cap. 11, pág. 799. Com ela podemos ver qual é o tipo de turbina, levando em conta a faixa de valores de Nsp para cada turbina mostrado na tabela, e comparando com o valor de Nsp encontrado.

Com o valor de 309,75, vemos que está dentro da faixa de valores para uma Turbina Francis.

Para avaliarmos o desempenho e compararmos com o desempenho da turbina Francis da figura 11.22, lá em cima, vamos calcular exatamente os 4 parâmetros que estão representados no gráfico da figura 11.22, que são os coeficientes de vazão, CQ, de altura de queda, CH, e de potência, CP, e também o rendimento da turbina, η.

As expressões para o cálculo de cada coeficiente são:

Onde,

-CQ é o coeficiente de vazão;

-Q é a vazão volumétrica do fluido;

-CH é o coeficiente de altura de queda;

-CP é o coeficiente de potência;

-g é constante da gravidade, 9,81 m/s2;

-ρ é a massa especifica (densidade) do fluido (água), que vale 1000 kg/m3 para a água;

-n é a rotação, em rps;

-Pe é a potência de eixo de saída de cada turbina;

-H é a altura de queda.

Calculando CQ

Calculando CH

Calculando CP

Só falta o rendimento para calcular.

O rendimento da turbina é a quantidade de potência que o equipamento gerou, Pe, dividido pela quantidade de potência disponível que a turbina tem para receber do fluido, PH, cuja expressão é

Onde,

-η é o rendimento da turbina;

-Pe é a potência de eixo de saída da turbina;

-PH é a potência hidráulica disponível, é a potência disponível que a turbina tem para receber do fluido;

O rendimento da turbina pode ser entendido também da seguinte forma: é a quantidade percentual de energia que a turbina recebeu do fluido, ou melhor, a quantidade percentual de energia que a turbina removeu do fluido, que escoa por dentro da turbina, para gerar a potência de eixo.

PH como foi dito, é a potência hidráulica disponível, e esta representa a quantidade total de energia disponível que o fluido possui para fornecer à turbina.

Essa variável, lembrando então, é função das propriedades do fluido e da vazão do fluido. A expressão para ela é a seguinte

Onde,

-ρ é a massa especifica (densidade) do fluido (água), que vale 1000 kg/m3 a 25ºC para a água;

-g é constante da gravidade, g=9,81 m/s2;

-Q é a vazão do fluido;

-H é a altura de queda;

Substituindo, a expressão para a eficiência agora é

Aplicando os valores

Analisando os valores em comparação com os da figura 11.22:

Vamos pegar os valores de CQ, CH e CP, no ponto de máximo rendimento e também o valor do rendimento máximo, para a turbina da figura 11.22

Onde, os coeficientes com (*) significam que são os valores dos coeficientes no ponto de máximo rendimento da turbina; e ηmáx é o rendimento máximo.

Comparando primeiramente os rendimentos, vemos que os valores são bem próximos, estando então as turbinas da usina com bons desempenhos em relação a rendimento.

Para os coeficientes, vemos que para CP e CQ, os valores obtidos são consideravelmente distantes dos valores da turbina Francis da figura. Com isso, estes parâmetros não estão próximos do ponto de máximo rendimento, podendo-se dizer que as variáveis de projeto potência e vazão não estão adequadas para uma operação ótima das turbinas dessa usina.

Para o coeficiente CH, o valor obtido foi bem próximo, estão esse parâmetro então próximo do ponto de máximo rendimento, como o valor da altura de queda apropriada ao projeto;