Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 94
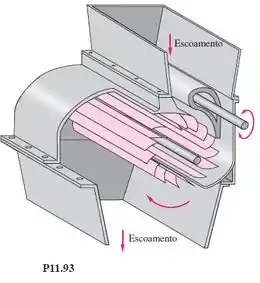
94 – Uma turbina simples de fluxo transversal, Figura P11.93, foi construída e testada na Universidade de Rhode Island. As pás foram feitas com tubos de PVC cortados logitudinalmente em três partes em arco de 120°. Quando ela foi testada em água a uma altura de queda de 1,62m e vazão de 39,75 l/s, a potência de eixo obtida experimentalmente foi de 0,6 hp. Calcule (a) o rendimento e (b) a rotação específica referente à potência, se n=200 rpm.
Passo 1
(A)
Vamos relembrar o rendimento e ver qual é sua expressão usual para cálculo.
O rendimento da turbina é a quantidade de potência que o equipamento gerou, Pe, dividido pela quantidade de potência disponível para a turbina receber do fluido, PH, cuja expressão é
Onde,
-η é o rendimento da turbina;
-Pe é a potência de eixo de saída da turbina;
-PH é a potência hidráulica disponível, é a potência que a turbina recebe do fluido;
O rendimento da turbina pode ser entendido também da seguinte forma: é a quantidade percentual de energia que a turbina recebeu do fluido, ou melhor, a quantidade percentual de energia que a turbina removeu do fluido, que escoa por dentro da turbina, para gerar a potência de eixo.
Passo 2
A potência de eixo de saída, Pe, lembrando, é a potência que é gerada pela turbina, que vai alimentar o gerador elétrico. Pelo enunciado, seu valor é de 0,6 hp.
Vamos agora revisar PH.
PH como foi dito, é a potência hidráulica disponível, e esta representa a quantidade total de energia disponível que o fluido possui para fornecer à turbina.
Essa variável, lembrando então, é função das propriedades do fluido e da vazão do fluido. A expressão para ela é a seguinte
Onde,
-ρ é a massa especifica (densidade) do fluido (água), que vale 1000 kg/m3 para a água;
-g é constante da gravidade, g=9,81 m/s2;
-Q é a vazão do fluido;
-H é a altura de queda;
Passo 3
Substituindo, a expressão para a eficiência agora é
Antes de substituirmos os valores, precisamos checar as unidades. A potência está em hp, e as demais variáveis estão em unidades do SI (m e kg), então para ficar equivalente em termos de unidades, você vai precisar converter a potência de hp para W (watts)
Onde, J=kgm2/s2.
Vamos converter hp para W, usando o seguinte fator de conversão
Assim,
Convertendo a vazão, Q, para m3/s:
Agora aplicando os valores
Passo 4
(B)
Para o cálculo da rotação especifica as unidades para cada variável deve ser as seguintes
Aplicando os valores
Resposta
A)
B)