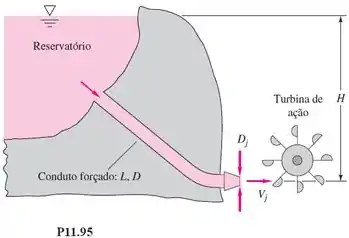
95 – Podemos fazer uma estimativa teórica do diâmetro apropriado para um conduto forçado de uma usina hidrelétrica em uma instalação com turbina de ação, como mostra a Figura P11.95. Admita L e H conhecidos e seja o desempenho da turbina idealizado pelas Equações (11.38) e (11.39). Considere as perdas por atrito hp no conduto forçado, mas despreze as perdas localizadas. Mostre que (a) é gerada a potência máxima quando hp=H/3, (b) a velocidade ótima do jato é (4gH/3)1/2 e (c) o melhor diâmetro do injetor é Dj=[D5/(2fL)]1/4, em que f é o fator de atrito do tubo.

Vamos começar com a equação para a potência de eixo da turbina.

A equação 11.38 do livro do White é uma derivação da equação para potência das equações de Euler das turbomáquinas, cuja expressão é

Onde,

-Pe é a potência desenvolvida pela turbina;

-ρ é a densidade da água, 1000 kg/m3;

-Q é a vazão;

-u2 é a velocidade periférica na entrada do rotor;

-u1 é a velocidade periférica na saída do rotor;

-Vt2 é a velocidade tangencial na entrada do rotor;

-Vt1 é a velocidade tangencial na saída do rotor;

Sendo que para uma turbina de ação, as velocidades periféricas são iguais

Onde, u é a velocidade linear da pá

Pela figura 11.26c do White, cap. 11, pág.801, você vai ver pelo diagrama de velocidades que podemos escrever as velocidades tangenciais, Vt, em termos da velocidade do jato, Vjato, e essas relações são as seguintes

Onde,

-Vjato é a velocidade do jato (Vjato=Vj da figura);

-u é a velocidade linear da pá da turbina;

-β é o ângulo da pá, na saída do jato;

Substituindo as relações das velocidades na Eq1

Onde,

-Pe é potência de eixo de saída;

-Vjato é a velocidade do jato;

-Q é a vazão volumétrica;

-u é a velocidade linear da pá da turbina;

-ρ é a densidade do fluido;

-β é o ângulo da pá, na saída do jato;

Essa Eq2 que encontramos é justamente a equação 11.38 do White.

Precisamos provar que a potência máxima ocorre para uma perda de carga, ou perda por atrito, hp, quando esta for igual a H/3.

Pela equação 11.39 do White, sabemos que na condição de potência máxima as velocidades do jato, Vjato, e linear da pá, u, se relacionam pela seguinte expressão

Substituindo na Eq2

Sendo Q a vazão volumétrica do fluido no injetor

A expressão para a vazão de um fluido em um injetor é

Onde,

-Q é a vazão volumétrica;

-Vjato é a velocidade do jato;

-Aj é a área do orifício do injetor;

O orifício do injetor é uma região circular, então sua área é a área de um circulo

Onde,

-Dj é o diâmetro de saída do injetor;

Substituindo

Substituindo essa última equação na Eq3

Fazendo

Fizemos isso para simplificar um pouco a resolução

Então,

Antes vamos relembrar Bernoulli:

A Eq. de Bernoulli, de forma direta, é referente a um balanço de energia mecânica entre dois pontos, que leva em consideração as variações de energia cinética, potencial e energia de pressão, além também da perda de energia por atrito. A expressão é

Onde,

-Δp é a variação de pressão do sistema;

-ΔV2 é a variação de energia cinética do sistema;

-Δz é a variação de energia potencial do sistema;

-hp é a perda de carga devido ao atrito do fluido com a tubulação;

-ρ é a densidade do fluido;

-g é a constante da gravidade, g=9,81 m/s2.

Aplicando o balanço de energia mecânica (Eq. de Bernoulli) entre o reservatório e a saída do injetor. Vamos denominar o ponto 1 sendo o reservatório e a saída do injetor como ponto 2.

Onde,

-p1 e p2 são a pressão do reservatório e da saída do injetor, respectivamente;

-V1 e V2 são a velocidade do fluido no reservatório e na saída do injetor, respectivamente;

-z1 e z2 são a altura no nível do reservatório e no nível da saída do injetor, respectivamente;

-hp é a perda de carga por atrito do fluido na tubulação;

Podemos reescrever a Eq. de Bernoulli assim

Vamos agora analisar a figura P11.95, lá em cima para ver quem é quem da equação de Bernoulli.

Analisando o esquema da figura P11.95, lá em cima, vamos ver que

Onde, patm é a pressão atmosférica que você pode considerar para as duas pressões, pois o reservatório está aberto para a atmosfera, assim também como na saída do injetor.

Já para as alturas z1 e z2 temos pela figura que

Onde,

-H é a diferença de altura entre o reservatório e a saída do injetor;

Também pela figura P11.95, vemos que

Já para V1, nós podemos considerar esta nula, pois a velocidade do fluido no ponto 1, que é no topo do reservatório, é muito pequena em relação a V2, devido ao tamanho do reservatório. Podemos demonstrar isso pela equação da continuidade

Onde,

-D1 e D2 são, respectivamente, o diâmetro do reservatório (DReserv) e o diâmetro do injetor (Dj);

Isolando V1

Como você pode ver pela figura P11.95 o tamanho do reservatório é muito maior do que a abertura do injetor, assim

Com isso, o termo dos diâmetros é praticamente zero

Consequentemente,

Portanto, a Eq. de Bernoulli agora é

Vamos relembrar perda de carga por atrito.

A perda de carga por atrito é a quantidade de energia que o fluido perde ao escoar pela tubulação devido ao atrito viscoso. Sua forma matemática é dada pela equação de Darcy-Weisbach:

Onde,

-hp é a perda de carga por atrito na tubulação;

-f é o fator de atrito;

-LT é o comprimento da tubulação;

-DT é o diâmetro da tubulação;

-VTubo é a velocidade do fluido na tubulação;

-g é a constante da gravidade, g=9,81 m/2.

Substituindo a equação da perda de carga na Eq5

Podemos relacionar a velocidade do fluido no tubo, VTubo, com a velocidade do jato pela equação da continuidade, que segue a seguinte expressão

Onde,

-Vjato é a velocidade do jato de água;

-VTubo é a velocidade da água no tubo;

-AT é a área de seção transversal do tubo;

-Aj é a área do orifício do injetor;

Lembrando que a área de uma circunferência é

Assim,

Isolando VTubo

Substituindo na Eq6

Substituindo lá na Eq4

Lembrando um pouco de máximos e mínimos, sabemos que para determinar um ponto de máximo de uma função, nós podemos derivar essa função e igualar a zero. Assim, vamos derivar a equação anterior da potência de eixo em relação a velocidade do jato.

Voltando lá em cima, temos que

Assim,

Substituindo

A solução então é

E pela equação de Darcy-Weisbach

Assim,

Portanto provamos que a potência máxima ocorre quando hp=H/3.

B)

Pegando a Eq5

Isolando Vjato

Como hp=H/3 no ponto ótimo, então

Também como foi pedido no enunciado, conseguimos demonstrar que a velocidade do jato segue a relação matemática acima no ponto de máxima potência.

C)

Nessa foi pedido para conferirmos se o diâmetro do injetor, Dj, no ponto ótimo (ponto de máxima potência) é dado pela expressão abaixo

Como já sabemos, no ponto ótimo temos que

E pela equação da continuidade, temos que

Isolando Dj

Também temos a seguinte relação

Substituindo,

Anulando as variáveis g e H

Passando DT para dentro do parêntese, para isso você deve elevar DT a 4ª potência dentro do parêntese

Então, chegamos na expressão apresentada no enunciado.