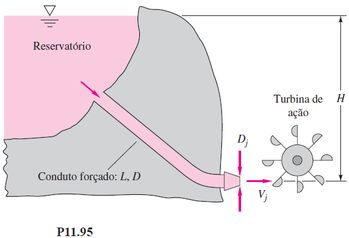
97 – Considere a seguinte versão não otimizada do Problema P11.95: H=450 m, L=5 km, D=1,2 m, Dj=20 cm. O conduto forçado é de concreto, e=1 mm. O diâmetro do rotor (DR) de ação é 3,2 m. Calcule (a) a potência gerada pelo rotor a 80% de rendimento e (b) a melhor rotação do rotor em rpm. Despreze as perdas localizadas.

Substituindo as relações das velocidades na Eq1

Onde,

-Pe é potência de eixo de saída;

-Vjato é a velocidade do jato;

-Q é a vazão volumétrica;

-u é a velocidade linear do rotor;

-ρ é a densidade do fluido (água), 998 kg/m3;

-β é o ângulo da pá, na saída do jato;

O valor de β normalmente aplicado na prática é de 165º, conforme a figura 11.26 do White, cap. 11, pág. 801.

A Eq2 assim como a Eq1 são equações para a potência de eixo gerada pela turbina válida para um rendimento da turbina de 100%. Neste problema o rendimento é de 80%. Devemos então acrescentar o termo do rendimento, η, na Eq2

A velocidade linear do rotor, u, se relaciona com a velocidade do jato, Vjato, matematicamente pela seguinte expressão

Essa expressão acima é na condição de máxima potência de eixo da turbina

Substituindo na Eq3

Olhando para a Eq4, você pode ver que falta a Vjato e a vazão, Q, que depende de Vjato, para você poder calcular a Pe.

Determinando a Vjato

Relembrando Bernoulli:

A Eq. de Bernoulli, de forma direta, é referente a um balanço de energia mecânica entre dois pontos, que leva em consideração as variações de energia cinética, potencial e energia de pressão, além também da perda de energia por atrito. A expressão é

Onde,

-Δp é a variação de pressão do sistema;

-ΔV2 é a variação de energia cinética do sistema;

-Δz é a variação de energia potencial do sistema;

-hp é a perda de carga devido ao atrito do fluido com a tubulação;

-ρ é a densidade do fluido;

-g é a constante da gravidade, g=9,81 m/s2.

Aplicando o balanço de energia mecânica (Eq. de Bernoulli) entre o reservatório e a saída do injetor, pela figura P11.95. Vamos denominar o ponto 1 sendo o reservatório e a saída do injetor como ponto 2

Onde,

-p1 e p2 são a pressão do reservatório e da saída do injetor, respectivamente;

-V1 e V2 são a velocidade do fluido no reservatório e na saída do injetor, respectivamente;

-z1 e z2 são a altura no nível do reservatório e no nível da saída do injetor, respectivamente;

-hp é a perda de carga por atrito do fluido na tubulação;

Podemos reescrever a Eq. de Bernoulli assim

Vamos agora analisar a figura P11.95, lá em cima para ver quem é quem da equação de Bernoulli.

Analisando o esquema da figura P11.95, lá em cima, vamos ver que

Onde, patm é a pressão atmosférica que você pode considerar para as duas pressões, pois o reservatório está aberto para a atmosfera, assim também como na saída do injetor.

Também vemos que

Também vemos que a velocidade em 1 é referente a velocidade de nível de fluido no reservatório, e você pode ver que ele é de grande dimensão (D muito alto), então a velocidade nesse ponto é muito pequena, devido justamente a essa grande dimensão do reservatório. Assim,

Já para as alturas z1 e z2, temos pela figura que

Onde,

-H é a diferença de altura entre o topo do reservatório e o injetor;

A Eq. de Bernoulli agora é

Vamos relembrar perda de carga por atrito.

A perda de carga por atrito é a quantidade de energia que o fluido perde ao escoar pela tubulação devido ao atrito viscoso. Sua forma matemática é dada pela equação de Darcy-Weisbach:

Onde,

-hp é a perda de carga por atrito na tubulação;

-f é o fator de atrito;

-LT é o comprimento da tubulação;

-DT é o diâmetro da tubulação;

-VTubo é a velocidade do fluido na tubulação;

-g é a constante da gravidade, g=9,81 m/2.

Substituindo,

Podemos relacionar a velocidade do fluido no tubo, VTubo, com a velocidade do jato pela equação da continuidade que é segue a seguinte expressão

Isolando VTubo

Substituindo na Eq6

Isolando Vjato

Precisamos agora encontrar o valor do fator de atrito para calcularmos DT.

O fator de atrito depende de Reynolds e da rugosidade relativa

Para conduto de concreto, a rugosidade, ε, vale

Lembrando que a Eq. de Reynolds é

Onde,

-ReD é o número de Reynolds;

-ρ é a densidade do fluido;

-DT é o diâmetro da tubulação;

-VTubo é a velocidade do fluido na tubulação;

-μ é a viscosidade dinâmica do fluido (água), μ=0,001 kg/m.s;

Como vimos mais acima, a velocidade do fluido no tubo, VTubo, se relaciona matematicamente com a velocidade do fluido no jato, Vjato, pela equação da continuidade

Substituindo a relação de VTubo na eq. de Reynolds

Você pode ver que Re precisa de Vjato, mas não temos Vjato que é o que queremos achar. Então, Re depende de Vjato, f depende de Re e Vjato depende de f, não podemos dessa forma determinar diretamente o valor de nenhum nem outro. O que temos que fazer é usar um método iterativo para encontrar a solução desse problema. Lembrando que um método iterativo você precisa dar um chute inicial para alguma das variáveis e a partir desse chute inicial você começa a calcular com as equações, pegando os valores calculados e atualizando o chute e recalculando novamente até que seja atingido uma convergência. Essa convergência você pode verificar da seguinte maneira: pegue o valor anterior calculado e diminua pelo novo valor calculado, estipule uma tolerância, ai quando essa diferença for menor que a tolerância você chegou em uma convergência.

• Algoritmo Resolução pelo método iterativo:

I – chute inicial para f (você pode olhar no diagrama de Moody a faixa de valores de f);

II – calcula Vjato pela equação

III – calcula Re pela equação

IV – determina novo valor de f usando diagrama de Moody ou Eq. de Churchill

V – calcula novo valor de Vjato pela mesma equação;

VI – calcular a diferença percentual (erro) entre o novo valor de Vjato com o valor anterior pela expressão

VII – verificar se erro é menor que a tolerância (estipular valor da tolerância, um valor muito pequeno se possível);

VIII – se o erro for maior que a tolerância, você volta a etapa III para uma nova iteração; (você vai continuar as iterações até que o erro seja menor que a tolerância)

Se você fizer este método iterativo à mão, vai levar algum trabalho. A melhor opção é usar um programa computacional, como o MATLAB, ou Python, ou até mesmo o EXCEL.

Para resolver eu usei o EXCEL, este é o mais simples. Abaixo o print do método no EXCEL.

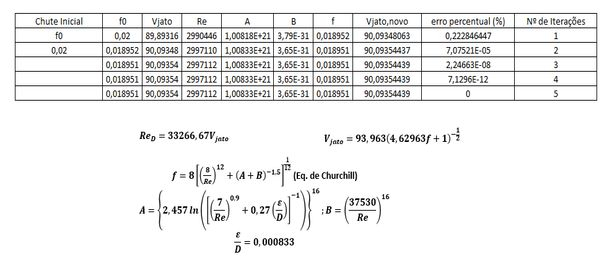
Veja pela imagem acima que na iteração de nº 2 já temos um erro percentual de 0,00007%, e também veja que o valor de Vjato, praticamente não se altera mais a partir dessa iteração. Portanto, houve uma convergência na iteração 2.

Os valores convergidos foram:

Calculando a vazão

Para calcularmos a vazão, temos que saber que aqui estamos calculando a vazão de um fluido que alimenta uma turbina de ação, e este tipo de turbina contém um injetor para o fluido. Assim, a vazão é função das variáveis associadas ao injetor.

A expressão para a vazão de um fluido em um injetor é

Onde,

-Q é a vazão volumétrica;

-Vjato é a velocidade do jato;

-Aj é a área do orifício do injetor;

O orifício do injetor é uma região circular, então sua área é a área de um circulo

Onde,

-Dj é o diâmetro de saída do injetor;

Substituindo

Aplicando os valores

Calculando a potência de eixo gerada pela turbina

Voltando a Eq4

Aplicando os valores

B)

Enfim, vamos calcular a rotação do rotor da turbina, n, em rpm.

Lembrando que a rotação de um rotor é diretamente proporcional a sua velocidade linear, seguindo a seguinte expressão

Onde,

-u é a velocidade linear do rotor;

-n é a rotação do rotor;

-DR é o diâmetro do rotor, DR=3,2m;

Já vimos antes que a velocidade linear, u, se relaciona com a velocidade do jato, Vjato pela expressão

Assim,

Isolando n

Aplicando os valores

Convertendo Rad/s para rpm (Rev/min):

Vamos relembrar que 1 revolução (Rev) é equivalente a 2πRad, assim

Assim,