O que aconteceria se tentássemos desacelerar um fluido supersônico com um difusor divergente?
Passo 1
E aí, como você está? Se você está se sentindo mal, saiba que você está melhor que o tradutor desse livro! Você pode estar se perguntando: “que grosseria é essa com o tradutor?”. A verdade é que o tradutor traduziu essa questão do texto original de forma errada! Para corrigir o enunciado, temos que mudar a palavra “desacelerar” pela palavra “acelerar”.

O enunciado certo seria: “O que aconteceria se tentássemos acelerar um fluido supersônico com um difusor divergente?”
Dito isso, vamos partir para o que realmente interessa, que é entender o que a questão quer! Essa questão é uma pegadinha sobre o que acontece com a velocidade de um fluido em escoamento supersônico, quando ele passa por um difusor divergente! A questão saber se conseguimos acelerar esse escoamento se ele atravessasse um difusor divergente!

E qual é a pegadinha? A pegadinha é que em escoamentos subsônicos (a velocidades menores que a velocidade do som ), a velocidade do fluido cai (o fluido desacelera) conforme ele atravessa o difusor divergente. A figura abaixo mostra a queda da velocidade subsônica!
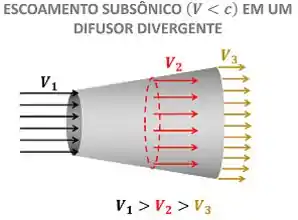
Como estamos mais acostumados a fazer questões sobre difusores divergentes subsônicos, ficamos tentados a dizer que o fluido desacelera para difusores supersônicos também!
No entanto, o resultado é o oposto! O fluido acelera (a velocidade do fluido aumenta), quando ele passa a uma velocidade maior que a velocidade do som por esse difusor!
No próximo passo explicamos o motivo!
Passo 2
Para entender o motivo do fluido acelerar em um escoamento subsônico, temos que lembrar da lei de conservação de massa para um difusor em regime permanente! Essa lei diz que a vazão em massa que entra no difusor é igual à vazão mássica que sai do difusor . Combinando essa informação com a equação de vazão mássica , achamos:
onde é a densidade do fluido, é a velocidade do fluido e é a área pela qual o fluido ta passando.
Reorganizando a equação acima, achamos uma equação para a velocidade de saída do fluido.
Como a área de saída do difusor é maior do que a área de entrada do difusor , podemos achar que era para a velocidade ser menor que a velocidade de entrada . No entanto, a densidade do fluido diminui muito conforme ele passa pelo difusor em um escoamento supersônico! Logo, é muito menor que ! é tão menor que que:
Em outras palavras, a velocidade de saída do fluido é maior do que a velocidade de entrada do fluido. Ou seja, o fluido acelera, quando passa por um difusor em escoamento supersônico!
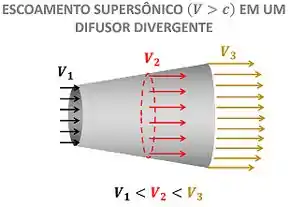
Logo, se tentássemos acelerar um fluido supersônico com um difusor divergente, acabaríamos alcançando o resultado desejado, porque, de fato, o escoamento supersônico acelera através desse difusor!
Resposta
Se tentássemos acelerar um fluido supersônico com um difusor divergente, acabaríamos alcançando o resultado desejado, porque, de fato, o escoamento supersônico acelera através desse difusor!