Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 49

Explique por que a taxa máxima de escoamento por unidade de área de determinado gás depende apenas de P 0 / T 0 . Para um gás ideal com k = 1,4 e R = 0,287   k J / k g K , encontre a constante a de forma que m ˙ / A * = a P 0 / T 0 .

Passo 1

O problema quer saber duas coisas:

  1. Por que a taxa máxima de escoamento m ˙ m á x (vazão mássica máxima) dividida pela a área A * da garganta do bocal convergente-divergente só depende da pressão de estagnação P 0 e da temperatura de estagnação T 0 ? Em outras palavras, o enunciado quer saber o motivo de m ˙ m á x / A * só variar com P 0 e T 0 . A imagem abaixo mostra essas variáveis.

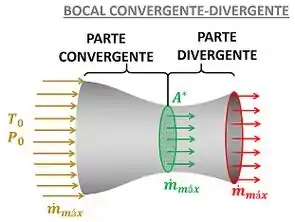
    2. Para chegar na resposta, temos que analisar a equação da vazão mássica máxima m ˙ m á x de um escoamento que atravessa um bocal convergente-divergente (equação 12-25 do livro).

    m ˙ m á x = A * P 0 k R T 0 2 k + 1 k + 1 2 k - 1

  2. Quanto vale a constante a que é igual a m ˙ m á x / A * dividido por P 0 / T 0 para um gás ideal com k = 1,4 e R = 0,287   k J / k g K ?

R é a constante de gás do fluido que atravessa o bocal e k é a razão entre os calores específicos c p e c v do fluido

a = m ˙ m á x / A * P 0 / T 0

Para responder essa pergunta, precisamos usar a mesma equação 12-25 do livro que usamos na pergunta anterior.

Passo 2

Nesse passo, vamos responder a primeira pergunta que listamos: por que m ˙ m á x / A * só varia com P 0 e T 0 ?

Para começar a analisar a equação 12-25 do livro e responder a pergunta, temos reorganizar a equação e entender o que significam os outros termos da nova equação.

m ˙ m á x = A * P 0 k R T 0 2 k + 1 k + 1 2 k - 1       ⟹     m ˙ m á x A * = P 0 k R T 0 2 k + 1 k + 1 2 k - 1

m ˙ m á x A * = P 0 T 0 k R 2 k + 1 k + 1 2 k - 1

onde R é a constante de gás do fluido que atravessa o bocal e k é a razão entre os calores específicos c p e c v do fluido.

k = c p / c v

Como chegamos nessa equação considerando os calores específicos c p e c v do gás com sendo constantes, k é constante. Ou seja, tirando o termo P 0 T 0 , todos os outros termos são constantes relacionadas ao fluido que está atravessando o bocal. Isso quer dizer que o valor dessas constantes k e R para o gás hélio H e é diferente do valor ar, mas elas não variam através do escoamento! m ˙ m á x A * só varia com P 0 T 0 , porque todos os outros termos são constantes do gás!

Passo 3

Nesse passo nós vamos responder a segunda pergunta que o enunciado faz: quanto vale a constante a que é igual a m ˙ m á x / A * dividido por P 0 / T 0 para um gás ideal com k = 1,4 e R = 0,287   k J / k g K ?

a = m ˙ m á x / A * P 0 / T 0 = ?

Para chegar nessa resposta, precisamos reorganizar a mesma equação 12-25 do livro que usamos na pergunta anterior.

m ˙ m á x A * = P 0 T 0 k R 2 k + 1 k + 1 2 k - 1       ⟹       m ˙ m á x A * P 0 T 0 ⏟ a = k R 2 k + 1 k + 1 2 k - 1       ⟹       a = k R 2 k + 1 k + 1 2 k - 1

Substituindo os valores de R e k na questão, achamos:

a = k R 2 k + 1 k + 1 2 k - 1       ⟹       a = 1,4 0,287 2 1,4 + 1 1,4 + 1 2 1,4 - 1       ⟹       a = 2,024   m K / s

Resposta

m ˙ m á x A * só varia com P 0 T 0 , porque todos os outros termos são constantes do gás.

a = 2,024   m K / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13-82C Como é definido o coeficiente de descarga C d das comportas basculantes? Quais são os valores normais deC d para as comportas basculantes com escoamento de saída livre? Qual é0 valor de C d par
13-79 Considere o escoamento da água em um canal com 10 m de largura a uma vazão de 70 mVs e uma profundidade de escoamento de 0,50 m. Agora a água sofre um salto hidráulico, ea profundidade de escoam
13-80 A profundidade do escoamento e a velocidade da água medidas após um salto hidráulico são 2 m e 3 m/s, respectivamente. Determine a profundidade e velocidade de escoamento antes do salto, e a fra
13-85C Considere o escoamento de um líquido sobre uma saliência durante o escoamento subcrítico em um canal aberto. A energia específica e a profundidade do escoamento diminuem sobre a saliência à med
13-86C O que é um reservatório de soleira espessa? Qual é a base de classificação dos reservatórios de soleira espessa?