Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 20
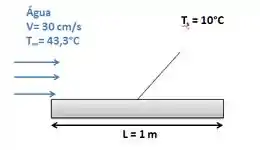
A água a 43,3°C escoa sobre uma grande placa, na velocidade de 30 cm/s. A placa tem 1,0 m de comprimento (na direção do escoamento), e sua superfície é mantida a uma temperatura uniforme de 10,0°C. Calcule a taxa permanente de transferência de calor por unidade de largura da placa.
Passo 1
Precisamos calcular o calor que está sendo transferido da água para a placa plana, e como sabemos, esse mecanismo de troca térmica é a convecção, então nossa equação principal para resolver o problema é:
O enunciado pede que calculemos a taxa por unidade de largura (W), certo? E essa largura vai aparecer como uma das variáveis que compõe a área de troca térmica. Então, se liga no que vamos fazer!
Não confunda esse W de largura como o W da unidade Watts que é destinada para taxa de troca de calor, beleza?
Passo 2
O próximo passo é a gente calcular h porque é a única varíavel que falta para encontrarmos o valor da taxa por unidade de largura, certo?
O início dos problemas de convecção é sempre tomarmos as propriedades dos fluidos na temperatura correta, e, para escoamentos externos, devemos pegar essas propriedades na temperatura de filme Tf !
Passo 3
Vamos calcular o valor de Reynold e definir o escoamento, já é?
Para mantermos Reynold adimensional, vamos passar essa velocidade de cm/s para m/s para estarmos sempre no SI.
Agora vamos descobrir se o escoamento é laminar, turbulento ou combinado...
Estamos abaixo do valor de reynold crítico e portanto esse escoamento é laminar!!
Passo 4
Agora vamos definir qual é a correlação mais apropriada para esse tipo de regime e a geometria de placa plana, belê?
TCHARÃÃÃ, ta aí ela:
Agora é ser feliz e substituir na nossa equação principal lá do passo 1 :D