Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 17

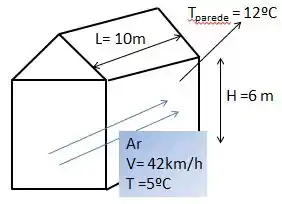
Durante um dia frio de inverno, o vento sopra a 42 km/h, paralelo à parede de uma casa de 6m de altura e 10m de comprimento. Considerando que o ar externo está a 5ºC e a parede está a 12ºC, determine a taxa de perda de calor por convecção dessa parede? Qual seria sua resposta se a velocidade do vento duplicasse?

Passo 1

Primeiro, vamos passar essa velocidade para SI.

V = 42 k m h 3,6 = 11,7 m s

Vamos pegar também as propriedades do fluido externo na temperatura apropriada, T f = 5 + 12 2 = 8,5 º C

K = 0,02428 W m . K

v = 1,413   x   10 - 5   m 2 s

P r = 0,73

Queremos calcular a taxa que sai da parede para o ar por convecção!!!!

q = h A ( T p a r e d e - T a r )

Passo 2

Vamos agora calcular o valor de reynold primeiramente como sendo

R e L = V L v = 11,7 x 10 1,413   x 10 - 5 = 8,26   x   10 6

Vamos usar a correlação de regime combinado porque estamos acima do Reynold crítico (que é o valor que inidica quando começamos a ter mudança de regime).

N u = h L K = 0,037 R e L 0,8 - 871 P r 1 / 3

h = K L 0,037 R e L 0,8 - 871 P r 1 / 3

h = 0,02428 10 0,037   8,26   x   10 6 0,8 - 871 0,73 1 3 = 25,8 W m 2 ° C

Substituindo na taxa por convecção e lembrando que a área de troca térmica é HxL, ou seja 60m²:

q = 25,8   x   10   x   6 12 - 5 = 10821   W

Passo 3

Se duplicarmos a velocidade, teremos:

v = 23,4 m s

Vamos seguir a mesma metodologia empregada na letra (a), ok?

Calculamos Reynold primeiro,

R e L = V L v = 23,4   x 10 1,413   x 10 - 5 = 1,651   x   10 7

Vemos que temos um escoamento combinado e vamos calcular h usando a melhor correlação que se enquadra dentro dessas condições.

N u = h L K = 0,037 R e L 0,8 - 871 P r 1 / 3

h = K L 0,037 R e L 0,8 - 871 P r 1 / 3

h = 0,02428 10 0,037   1,651   x   10 7 0,8 - 871 0,73 1 3 = 46 ,   28 W m 2 ° C  

Substituindo na taxa, obtemos por fim:

q = 46,28   x   10   x   6 12 - 5 = 19440   W

ISSO SEMPRE VAI ACONTECER!!! Toda vez que você tiver um escoamento com maior velocidade com o mesmo fluido e mesmas outras condições, sempre espere encontrar um valor de h e q maiores. Resumindo, quanto mais turbulento o regime, melhor será a troca térmica.

Resposta

  1. q =10821 W (b) q = 19440 W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

55 – Considere o escoamento de um fluido sobre um cilindro mantido a uma temperatura constante. Agora, a velocidade do escoamento livre do fluido é duplicada. Determine a mudança na força de arrasto n
58 – Uma linha de transmissão elétrica de 5m m de diâmetro transporta uma corrente elétrica de 50A e tem resistência de 0,002o h m por metro de comprimento. Determine a temperatura da superfície do fi
56 – Um longo tubo de vapor de 12c m de diâmetro cuja temperatura da superfície externa é 90℃ ℃ passa por uma área aberta sem proteção contra ventos. Determine a taxa de perda de calor do tubo por uni
57 -Em uma usina geotérmica, a água geotérmica utilizada a 80℃ ℃ entra em um tubo não isolado de 15c m de diâmetro e 400m de comprimento a uma taxa de 8,5k g / s e o deixa a 70℃ ℃, antes de voltar a s
53 – Reconsidere o Prob. 7-52. Usando EES (ou outro ar e da velocidade do vento variar sobre a taxa de perda de calor a partir do braço. Deixe a temperatura do ar variar entre - 5℃ ℃ e 25℃ ℃ e a veloc