Água entra em um tubo a 27°C com uma vazão de . A transferência de calor da parede do tubo para o fluido é dada pela expressão , sendo o coeficiente a igual a e x(m) é a distância axial para a entrada do tubo.
- Partindo de um volume de controle diferencial propriamente definido, deduza uma expressão para a distribuição de temperaturas na água.
- Qual é a temperatura de saída da água para uma seção aquecida com 30 m de comprimento?
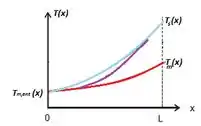
- Esboce o comportamento da temperatura média do fluido, , e da temperatura da parede do tubo, , como uma função da posição ao longo do tubo, para condições de escoamento plenamente desenvolvido e de escoamento em desenvolvimento.
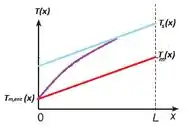
- Qual valor de um fluxo térmico na parede uniforme,, (em vez de ), iria fornecer uma temperatura do fluido na saída do tubo igual à determinada na parte (b)? Para esse tipo de aquecimento, esboce as distribuições de temperaturas solicitadas na parte (c).
Passo 1
Faaaaaaaaaaaaalaa meus queridos, bora seguir?
Na letra (a) nós precisamos definir o volume de controle, certo?
Então bora desenhar e ver o que está acontecendo:
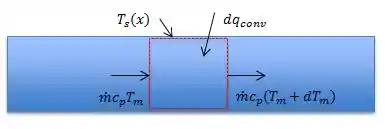
Fazendo o balanço energético:
Podemos reescrever a variação do calor convectivo como:
Então:
Lembrando que:
Nossa equação ficará assim:
Como queremos uma função para , o que precisamos ?
Integrar, certo?
Isolando a temperatura no ponto
Terminamos a letra (a) e vamos seguindo pra (b)!!
Passo 2
Na letra (b) nós precisamos achar a temperatura de saída da água para uma seção aquecida com 30 m de comprimento.
Então:
Para a água a 300 K podemos olhar a Tabela A.6:
Substituindo na equação do Passo 1:
É isso aí chegamos ao fim da letra (b) !!
Passo 3
Na letra (c) nós devemos esboçar o comportamento da temperatura média do fluido, , e da temperatura da parede do tubo, , como uma função da posição ao longo do tubo, para condições de escoamento plenamente desenvolvido e de escoamento em desenvolvimento
Nós sabemos que:
Uma parábola em relação a distância,
Mas nós também queremos saber como se comporta e, para isso, nós vamos usar a equação para a troca de calor convectivo:
Isso nos trás uma relação entre as duas, certo?
Beleza!!
Quando o escoamento é completamente desenvolvido o coeficiente convectivo é constante, então à medida que a distância x aumenta, a diferença, também vai aumentar de maneira linear.
Quando temos o escoamento em desenvolvimento, o coeficiente vai decrescer com a distância até atingir o desenvolvimento completamente desenvolvido.
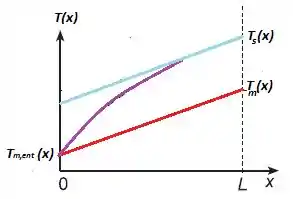
Postando estes dados em um gráfico:
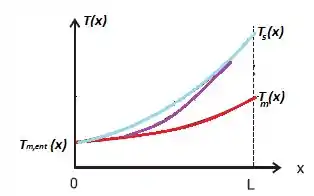
Aqui, a curva vermelha representa a parábola para A curva em azul representa para o escoamento completamente desenvolvido, percebem que a distância entre as temperaturas aumenta, certo?
A linha em roxo representa o escoamento em desenvolvimento, alcançando o escoamento completamente desenvolvido quando
Passo 4
Para a letra (d) nós precisamos lembrar lá do Passo 1:
O calor também pode ser escrito em função de :
Igualando:
Então nós temos o fluxo de calor em função do diâmetro específico do tubo.
Como o fluxo aqui não foi dado em função de x, quando integrarmos a equação lá do Passo 1:
E olhando o Passo 3:
Portanto também é linear devido ao componente
Analogamente ao caso anterior:
E o que acharam desta?