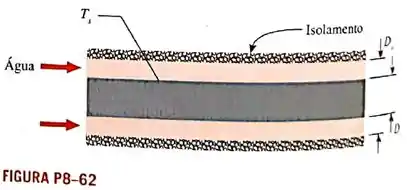
Água escoa com vazão mássica de por um tubo anelar concêntrico a uma temperatura média de entrada e de saída de e , respectivemente. O tubo anelar concêntrico tem diâmetro interno e externo de e , respectivemente. A parede interna do tubo é mantida a uma temperatura de superfície constante de , enquanto a superfície externa do tubo é isolada. Determine o comprimento do tubo anelar concêntrico.

Podemos obter uma relação para a velocidade média do fluxo. Assim temos:

Aqui,  é o diâmetro externo do tubo anular,  é o diâmetro interno do tubo anular e  é a taxa de fluxo de massa.

Com a velocidade média, podemos calcular o número de Reynolds usando a seguinte relação.

Substituindo a velocidade média, temos:

Substituindo os termos pelos dados fornecidos no enunciado, temos:

Como o número de Reynolds é superior a , o fluxo através do anel é turbulento.

Agora, vamos calcular Nusselt, para isso, podemos usar a relação de Dittus-Boelter. Assim temos:

Substituindo os termos da equação pelos dados fornecidos, temos:

Com o número de Nusselt, podemos calcular o coeficiente de transferência de calor por convecção da seguinte maneira:

Substituindo os termos da equação pelos dados fornecidos, temos:

Agora, podemos calcular o comprimento do tubo de anel concêntrico usando a seguinte relação:

Aqui,  é a temperatura da superfície do tubo interno,  é o calor específico da água, é a temperatura média da agua na entrada, é a temperatura média da água na saída. Substituindo os termos da equação pelos dados fornecidos, temos:

Portanto, o comprimento do tubo de anel concêntrico é .