Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 12.Problemas - Ex. 53

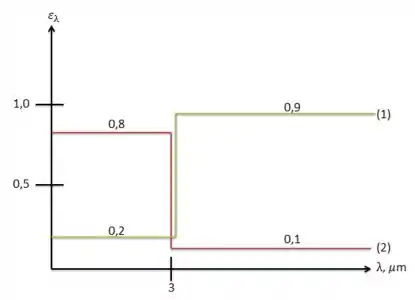
As variações da emissividade espectral de duas superfícies são indicadas na figura a seguir. Determine a emissividade média de cada superfície a T =3.000 K. Além disso, determine a absortividade e a refletividade média de cada superfície para a radiação proveniente de uma fonte a 3.000 K. Qual superfície é mais adequada como absorvedor solar?

Passo 1

Então, temos dois materiais, que vamos chamar de (1) e (2), com diferentes perfis de emissividade. A partir dos perfis devemos encontrar a emissividade média de cada um na temperatura de T = 3.000 K, além da respectiva absortividade e refletividade. No final, seremos capazes de responder qual material é mais adequado para utilizar como absorvedor solar. Vamos lá??

Passo 2

Vamos começar escrevendo o perfil de emissividade do material (1):

ε λ = ε 1 = 0,2 ,               0 ≤ λ < 3   μ m ε 2 = 0,9 ,             3   μ m ≤ λ < ∞

A partir do perfil iremos calcular a emissividade média da superfície (1). A emissividade média pode ser calculada por:

ε T = ∫ 0 ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 3   μ m ε λ λ , T E b λ λ , T d λ + ∫ 3   μ m ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 3   μ m 0,2 x E b λ λ , T d λ + ∫ 3   μ m ∞ 0,9 x E b λ λ , T d λ σ T 4

ε T = 0,2 x ∫ 0 3   μ m E b λ λ , T d λ + 0,9 x ∫ 3   μ m ∞ E b λ λ , T d λ σ T 4

ε T = 0,2 x ∫ 0 3   μ m E b λ λ , T d λ + 0,9 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 3   μ m E b λ λ , T d λ ) σ T 4

Podemos aproximar ∫ 0 λ E λ , b d λ utilizando a função de radiação f λ :

∫ 0 λ E λ , b d λ = σ T 4 f λ

Vamos usar isso para encontrar a emissividade hemisférica total:

ε T = 0,2 x ∫ 0 3   μ m E b λ λ , T d λ + 0,9 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 3   μ m E b λ λ , T d λ ) σ T 4

ε T = 0,2 x σ T 4 x f 0 - 3   μ m + 0,9 x σ T 4 x ( f 0 - ∞ - f 0 - 3   μ m ) σ T 4

ε T = 0,2 x f 0 - 3   μ m + 0,9 x ( f 0 - ∞ - f 0 - 3   μ m )

Pela tabela 12-2 do capítulo do livro temos que para:

∞ x T → f = 1

3   μ m   x   3.000   K = 9.000   μ m . K → f = 0 , 890029

Então, nossa emissividade é:

ε T = 0 , 2 x 0 , 890029 + 0 , 9 x ( 1 - 0 , 890029 )

ε T 1 = 0 , 277

Temos agora que determinar a absortividade e refletividade do material (1). Para isso, vamos utilizar a lei de Kirchhoff. Esta lei define que:

ε = α

Então, a absortividade para 3.000 K é α 1 = 0,277. Precisamos ainda da refletividade. Para qualquer corpo:

α + ρ + τ = 1

Considerando que a superfície é opaca → τ = 0 . Portanto:

α + ρ + 0 = 1

ρ 1 = 1 - α 1

ρ 1 = 1 - 0 , 277

ρ 1 = 0 , 723

Passo 3

Agora vamos fazer o mesmo procedimento para a superfície (2). Vamos começar escrevendo o perfil de emissividade do material (2):

ε λ = ε 1 = 0,8 ,               0 ≤ λ < 3   μ m ε 2 = 0,1 ,             3   μ m ≤ λ < ∞

A partir do perfil iremos calcular a emissividade média da superfície (2). A emissividade média é calculada por:

ε T = ∫ 0 ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 3   μ m ε λ λ , T E b λ λ , T d λ + ∫ 3   μ m ∞ ε λ λ , T E b λ λ , T d λ σ T 4

ε T = ∫ 0 3   μ m 0,8 x E b λ λ , T d λ + ∫ 3   μ m ∞ 0,1 x E b λ λ , T d λ σ T 4

ε T = 0,8 x ∫ 0 3   μ m E b λ λ , T d λ + 0,1 x ∫ 3   μ m ∞ E b λ λ , T d λ σ T 4

ε T = 0,8 x ∫ 0 3   μ m E b λ λ , T d λ + 0,1 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 3   μ m E b λ λ , T d λ ) σ T 4

Podemos aproximar ∫ 0 λ E λ , b d λ utilizando a função de radiação f λ :

∫ 0 λ E λ , b d λ = σ T 4 f λ

Vamos usar isso para encontrar a emissividade média:

ε T = 0,8 x ∫ 0 3   μ m E b λ λ , T d λ + 0,1 x ( ∫ 0 ∞ E b λ λ , T d λ - ∫ 0 3   μ m E b λ λ , T d λ ) σ T 4

ε T = 0,8 x σ T 4 x f 0 - 3   μ m + 0,1 x σ T 4 x ( f 0 - ∞ - f 0 - 3   μ m ) σ T 4

ε T = 0,8 x f 0 - 3   μ m + 0,1 x ( f 0 - ∞ - f 0 - 3   μ m )

Pela tabela 12-2 do capítulo do livro temos que para:

∞ x T → f = 1

3   μ m   x   3.000   K = 9.000   μ m . K → f = 0,890029

Então, nossa emissividade é:

ε T = 0,8 x 0,890029 + 0,1 x ( 1 - 0,890029 )

ε T 2 = 0,723

Temos agora que determinar a absortividade e refletividade da superfície (2). Para isso, vamos utilizar a lei de Kirchhoff. Esta lei define que:

ε = α

Então, a absortividade para 3.000 K é α 2 = 0,723. Precisamos ainda da refletividade. Para qualquer corpo:

α + ρ + τ = 1

Considerando que a superfície é opaca → τ = 0 . Portanto:

α + ρ + 0 = 1

ρ 2 = 1 - α 2

ρ 2 = 1 - 0,723

ρ 2 = 0,277

Resposta

Como α 2 > α 1 significa que a superfície (2) tem maior capacidade de absorver a irradiação do Sol e, por isso, o material (2) é o mais adequado para usarcomo absorvedor solar.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno objeto opaco e difuso, a T s = 5 00K , está suspenso em um grande forno cujas paredes internas estão a T f = 2 5 00K . As paredes são difusas e cinzas, e têm uma emissividade de 0 , 37 . A
Dois revestimentos especiais estão disponíveis para aplicação em uma placa de absorção instalada abaixo da cobertura de vidro descrita no Exemplo 12.9. Cada um dos revestimentos é difuso e caracteriza
Uma amostra muito pequena de uma superfície opaca encontra-se inicialmente a 1200K e tem a absortividade hemisférica espectral mostrada na figura.A amostra é colocada no interior de um grande comparti
Considere uma superfície difusa e opaca com a absortividade espectral e a irradiação apresentadas a seguir:Qual é a absortividade total da superfície para a irradiação especificada? Se a superfície se
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral d