Considere um fluido com número de Prandtl de escoando em um tubo circular liso. Usando as equações do Colburn, Petukhov, e Gnielinski, determine os números de Nusselt para números de Reynolds de , e . Compare e discuta os resultados.
Passo 1
Primeiramente devemos listar as equações solicitadas no enunciado, que são:
Onde,
Onde,
Passo 2
Calculando os números de Nusselt, teremos que...
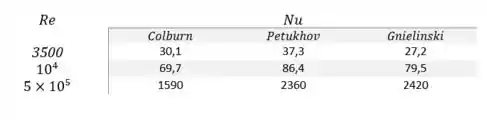
Resposta
Discutindo a respeito das equações, nós temos que a equação de Gnielinski é preferida nos cálculos, pois possui maior precisão.
Na região de transição (Re = 3500), a equação de Colburn teve um desempenho melhor que a equação de Petukhov. Quando comparada com a equação de Gnielinski em Re = 3500, a equação de Colburn superestimou o Nu em cerca de 11%, enquanto a equação de Petukhov superestimou o Nu em cerca de 37%.
Quando comparada com a equação de Gnielinski em Re = , a equação de Colburn subestimou o Nu em cerca de 12%, enquanto a equação de Petukhov superestimou o Nu em cerca de 9%.
Quando comparada com a equação de Gnielinski em Re = , a equação de Colburn subestimou o Nu em cerca de 34%, enquanto a equação de Petukhov subestimou o Nu em cerca de 3%. A equação de Petukhov comparou melhor que a equação de Colburn na região turbulenta ().