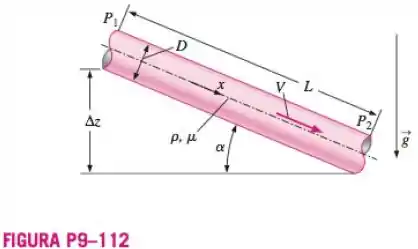
Água flui através de um tubo inclinado, longo e reto, de diâmetro  e comprimento  (Figura P9-112). Não há nenhum gradiente de pressão entre os pontos e ; em outras palavras, a água flui através do tubo apenas pela gravidade, e  . O escoamento é permanente, completamente desenvolvido e laminar. Adotamos um sistema de coordenadas na qual  segue o eixo do tubo.  Use a técnica do volume de controle do Capítulo 8 para encontrar uma expressão para a velocidade média  como uma função dos parâmetros dados , , , ,  e .  Use a análise dimensional para gerar uma expressão adimensional para  como uma função dos parâmetros dados. Compare com o resultado da parte e discuta.  Use a análise dimensional para gerar uma expressão adimensional para  em função dos parâmetros dados. Construa uma relação entre seus que corresponda à expressão analítica exata.

(a) Aqui, foi pedido para encontramos uma expressão para a velocidade média em função de , , , ,  e . Usando a técnica do volume de controle, temos que a equação da energia pode ser escrita da seguinte maneira:

Foi dito no enunciado que o escoamento é totalmente desenvolvido, assim, podemos dizer que

Também foi dito no enunciado que a pressão no ponto 1 é igual a pressão no ponto 2 que é igual a pressão atmosférica, ou seja:

Substituindo as duas observações feitas na equação da energia, temos o seguinte:

Com isso, podemos simplificar cortando os termos iguais dos dois lados da igualdade, assim temos:

Para esse tubo inclinado, temos que a perda de carga é dada por:

Para o fluxo laminar, o fator de atrito de Darcy é dado por:

Também podemos escrever o Número de Reynolds como:

Assim, podemos dizer que:

Substituindo o fator de atrito na perda de carga, temos:

Agora, vamos substituir a perda de carga na equação da energia simplificada encontrada no passo 3. Assim temos:

Reorganizando para encontrar a velocidade media, temos:

Portanto, a velocidade média é dada por

(b) Para podermos resolver a questão, precisamos fazer algumas hipóteses.

Pelo desenho fornecido no enunciado, podemos dizer que o escoamento ocorre apenar na direção de .

Também, vamos assumir o fluxo como fluxo newtoniano, assim, o campo de velocidade é assumido como axissimétrico, ou seja,  implicando que todas as derivadas em relação a são zero. 

Temos também que o fluxo é assumido como paralelo, ou seja, .

Vamos assumir uma condição de não escorregamento na parede do tubo, isso implica que quando , a velocidade é .

Temos que a linha central do tubo é um eixo de simetria. Então, em  temos que .

Feitas as suposições, vamos pegar a equação de continuidade incompressível em coordenadas cilíndricas  e . Temos que á equação é a seguinte:

Agora, vamos substituir as os termos da equação acima pelas suposições feitas anteriormente. Assim temos que:

Ao integrarmos, temos vamos encontrar que:

Agora, vamos pegar a componente  da equação de Navier-Stokes incompressível. Assim temos:

Substitua as condições por nós assumidas, temos que a equação acima fica da seguinte forma:

Podemos escrever a gravida em como . Substituindo, temos:

Agora, vamos reescrever a equação encontrada no passo anterior da seguinte maneira:

Pela equação (1), sabemos que a velocidade axial  é uma função apenas de . Assim, podemos escrever como a equação acima como

Agora, podemos integrar equação acima com relação a . Logo, temos o seguinte:

Pela suposição feita anteriormente que em  temos que , podemos dizer o seguinte:

Para que a suposição seja atendida, precisamos que . Assim temos que a equação se torna a seguinte:

Agora, vamos integrar a equação acima mais uma vez em relação a . Assim temos que:

Vamos usar a outra suposição feita anteriormente que diz que em ,  a velocidade zero. Assim, temos que:

Substituindo encontrado na equação, temos:

Agora, podemos dizer que a taxa de fluxo de volume através do tubo é a seguinte:

Temos que o diferencial de área de um tubo círculo é .

Substituindo a velocidade na expressão acima, temos:

Podemos escrever a velocidade media através do tubo pela seguinte expressão:

Substituindo o fluxo de volume e a área na expressão acima, temos:

Podemos dizer que e . Assim, substituindo na expressão acima, temos:

Portanto, velocidade através do tubo é dada por

Podemos perceber que resultado obtido na letra e na letra são iguais.

(c) Aqui existem variáveis ​​e dimensões principais. Portanto, exigimos  parâmetros sem dimensão. Os parâmetros adimensionais são: