Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 52
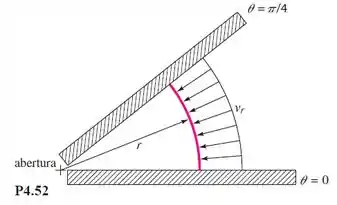
Um fluido sem atrito, incompressível, bidimensional é guiado, por duas paredes dispostas em forma de cunha, para uma pequena abertura na origem, como mostra a Figura P4.52. A largura na direção perpendicular ao papel é b, e a vazão volumétrica é Q. Em qualquer distância dada r a partir da abertura, o escoamento é radial para dentro, com velocidade constate. Encontre uma expressão para a função corrente em coordenadas polares desse escoamento.
Passo 1
Eita! Simbora lá pra mais uma!
Okay, podemos encontrar a velocidade radial disso ai usando a equação da continuidade, olha só:
Da equação 4.101, teremos então que:
Assim, por separação de variáveis:
em que C é uma constante!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um cilindro circular é equipado com dois sensores de pressão de superfície para medir p a em θ =180 oep b em θ =105 o . A intenção é usar o cilindro como um anemômetro. Usando a teoria não viscosa, de
Vento a U ∞ e p ∞ escoa em torno de uma cabana Quonset, que é um semicilindro de raio a e comprimento L (Figura P8.48). A pressão interna é pi. Usando a teoria não viscosa, deduza uma expressão para a
Deseja-se simular o escoamento em torno de uma colina ou saliência bidimensional usando uma linha de corrente que passa acima do escoamento sobre um cilindro, como na Figura P8.50. A saliência deve te
Um cilindro é formado por fixação de dois canais semicilíndricos com pinos internos, como mostra a Figura P8.46. Existem 10 pinos por metro de largura de cada lado, e a pressão interna é de 50 kPa (ma
Considere água a 20 o C escoando a 6 m/s em torno de um cilindro circular de 1 m de diâmetro. Qual a intensidade λ do dipolo, em m³/s, necessária para simular esse escoamento? Se a pressão da corrente