Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 68
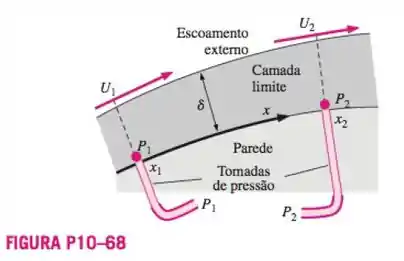
A pressão estática P é medida em duas posições ao longo da parede de uma camada limite laminar (Figura P10-68). As pressões medidas são e e a distância entre as tomadas de pressão é pequena comparada com a dimensão característica do corpo . A velocidade do escoamento externo acima da camada limite no ponto 1 é . A densidade e a viscosidade do fluido são e , respectivamente. Gere uma expressão aproximada para , a velocidade do escoamento externo acima da camada limite no ponto 2, em termos de , , , e .
Passo 1
Beleza! A primeira coisa que devemos lembrar é que pela aproximação da camada limite, a pressão é constante quando normal à camada limite, mas não é necessariamente constante ao longo do comprimento da camada limite. Então, com isso, para qualquer linha de corrente ao longo da camada limite, a pressão na região superior do escoamento externo é a mesma daquela na parede do escoamento.
Agora, aplicando a equação de Bernoulli para a região do escoamento externo, com o auxílio da equação 10-86 vista nesse capítulo, temos:
Passo 2
Agora, para pequenos valores de , que é o nosso caso, conforme dito no enunciado, podemos aproximar a velocidade como:
Isolando a expressão dessa expressão, chegamos em:
Da mesma forma, para pequenos valores de , a pressão pode ser escrita como:
Isolando a expressão , chegamos em:
Passo 3
Agora então nós vamos substituir as expressões para e encontradas no passo 2 na expressão encontrada lá no passo 1, de modo que teremos:
Isolando dessa expressão, chegamos em:
Prooonto! Chegamos na expressão que queríamos encontrar.