Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 121

A água quente a 60°C é resfriada a 36°C através do lado do tubo de um trocador de calor com um passe no casco e 2 passes no tubo. O fluido de resfriamento também é a água, para a qual as temperaturas de entrada e saída são 7°C e 31°C, respectivamente. O coeficiente global de transferência de calor e a área de transferência de calor são 950 W m 2 K e 15 m², respectivamente. Calcule as vazões mássicas da água quente e fria em operação permanente.

Passo 1

Shoow galeraa !!

Vamos continuando...

Bom, nós queremos as vazões mássicas, certo? E já sabemos qual fórmula usar:

Q ˙ = m q ˙ c p ( T q ,   e n t r a - T q ,   s a i )

Q ˙ = m f ˙ c p ( T f ,   s a i - T f ,   e n t r a )

Lembrando que:

c p = 4 , 18 k J k g K

T q ,   e n t r a = 60 ° C

T q ,   s a i = 36 ° C

T f ,   e n t r a = 7 ° C

T f ,   s a i = 31 ° C

Mas para achar as vazões nós precisamos da taxa de transferência de calor, e para isso nós podemos usar:

Q ˙ = U F A s ∆ T l m

Já sabemos que:

U = 950 W m 2 K

A s = 15   m ²

Mas nada sobre F e ∆ T l m , certo?

Começando pela diferença média logarítima:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Se:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,   s a i - T f ,   e n t r a

Podemos só substituir:

∆ T 1 = 6 0 ° C - 31 ° C = 29 ° C

∆ T 2 = 36 ° C - 7 ° C = 29 ° C

Como ∆ T 1 = ∆ T 2 podemos assumir que:

∆ T l m = 29 ° C

Passo 2

O nosso próximo passo é calcular o fator de correção, F, vamos precisar olhar a figura:

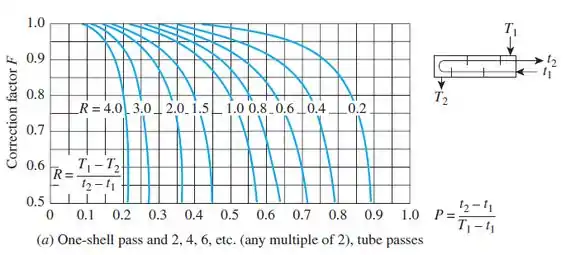
Vamos começar calculando R e P:

R = T q ,   e n t r a - T q ,   s a i T f ,   s a i - T f ,   e n t r a = 6 0 ° C - 36 ° C 31 ° C - 7 ° C = 1

P = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a = 31 ° C - 7 ° C 6 0 ° C - 7 ° C = 0 , 4 5

Então:

F ≅ 0 , 88

Agoora siiim !!

Vamos colocar tudo isso na fórmula do calor:

Q ˙ = 950 W m 2 K 0,88 15   m 2 29 ° C

Q ˙ = 363660   W

Ou melhor:

Q ˙ = 363,66   k W

Passo 3

Achamos o calor trocado e agoora sim podemos calcular as vazões mássicas:

363,66   k W = m q ˙ 4,18 k J k g K ( 60 ° C - 36 ° C )

m q ˙ = 3,625 k g s

363,66   k W = m f ˙ 4,18 k J k g K ( 31 ° C - 7 ° C )

m f ˙ = 3,625 k g s

Ou melhor:

m q ˙ = m f ˙ = 3,625 k g s

E terminamos mais uma galerinha !!

Resposta

m q ˙ = m f ˙ = 3,625 k g s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34 - Explique como o método LMTD pode ser utilizado para determinar a superfície de transferência de calor de um trocador de calor de tubos e casco de várias passagens quando todas as informações nece
35 - Na relação de transferência de calor Q ˙ = A s U F ∆ T l m para um trocador de calor como a quantidade F échamada?O que isso representa?Fpodeser maior que um?
42 - Uma escoamento de hidrocarboneto c p =2,2k J /k g · K é resfriada a uma taxa de 720k g / h de 150° C a 40° C no lado do tubo de um trocador de calor de tubo duplo em contracorrente.A água c p = 4
44 - Um trocador de calor de escoamento paralelo de tubo duplo deve aquecer a água c p = 4,18 J k g ⋅ K de 25° C a 60° C a uma taxa de 0,2k g / s .O aquecimento deve ser realizado com água geotérmica
38 - Um trocador de calor de contracorrente é indicado para ter o coeficiente de transferência global de transferência de calor de 284W / m 2 ⋅ K quando operando o projeto em condições limpas.O fluido