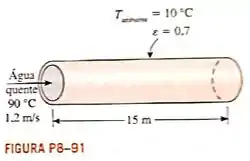
Água quente a entra na seção de de um tubo de ferro fundido cujos diâmetros interno e externo são e , respectivamente, com velocidade média de . A superfície externa do tubo, cuja emissividade é , está exposta ao ar frio a no porão, com coeficiente de transferência de calor por convecção de . Considerando que as paredes do porão estão igualmente a , determine a taxa de perda de calor a partir da água e a temperatura em que a água sai do porão.

Como o tubo não é muito comprido, vamos assumir que a temperatura média da água é . Verificaremos essa suposição mais tarde.

Agora, vamos consultar a tabela A-9, 'Propriedades da água saturada' para obter algumas propriedades da água à temperatura média de .

Densidade:  

Calor específico:  

Condutividade térmica:  

Viscosidade dinâmica:  

Número Prandtl:  

a) Para resolver essa questão, podemos começar calculando o número de Reynolds usando a seguinte expressão:

Aqui, é a velocidade média do fluido e o diâmetro interno do tubo. Substituindo os termos da equação pelos dados coletados, temos:

Como o número de Reynolds é maior que  o fluxo é turbulento.

Vamos agora calcular os comprimentos de entrada neste caso. Assim temos:

Como o comprimento da entrada é muito menor que o comprimento especificado do tubo. Portanto, é um fluxo turbulento totalmente desenvolvido em todo o tubo.

Podemos encontrar no diagrama de Moody Figura A-20, a rugosidade do tubo de ferro fundido.

Podemos calcuar o fator de atrito usando a seguinte expreção:

Agora, podemos calcular o número de Nusselt usando expressão de Chilton-Colburn.

Substituindo os termos da equação pelos dados coletados e calculados, temos:

Podemos calcular o coeficiente de transferência de calor por convecção usando a relação para o número de Nusselt.

Aqui,  é o coeficiente de transferência de calor por convecção. Substituindo os termos da equação pelos dados coletados e calculados, temos:

Temos que o coeficiente de transferência de calor por convecção dentro do tubo é muito superior ao coeficiente de transferência de calor por convecção no exterior de . Portanto, a resistência térmica da convecção no interior do tubo é insignificante e, portanto, a temperatura da superfície interna do tubo pode ser considerada igual à temperatura da água. Além disso, esperamos que o tubo seja quase isotérmico, uma vez que é feito de metal fino (verificamos isso mais tarde). Então a taxa de perda de calor do tubo será a soma da convecção e radiação da superfície externa a uma temperatura de .

Agora, vamos calcular a resistência térmica dentro do tubo usando a seguinte expressão:

Aqui,  é o diâmetro externo do tubo,  é o diâmetro interno do tubo,  é a condutividade térmica do tubo e  é o comprimento do tubo. Substituindo os termos da equação pelos dados coletados, temos:

Como a resistência térmica no interior do tubo é muito pequena, podemos dizer que a temperatura externa e interna será quase igual. Isso vai de acordo com a suposição feira no passo anterior.

Portanto, a temperatura da superfície do tubo é

Precisamos calcular a área da superfície externa do tubo, pois vamos precisar futuramente. Assim temos:

Aqui,  é a área da superfície externa do tubo. Substituindo os termos da equação pelos dados coletados, temos:

Vamos calcular também a área da seção transversal do tubo.

Aqui, é a área da seção transversal do tubo,  é o diâmetro interno do tubo. Substituindo os termos da equação pelos dados coletados, temos:

Também vamos calcular a vazão mássica.

Aqui  é a vazão mássica. Substituindo os termos da equação pelos dados coletados, temos:

Agora, podemos calcular a taxa total de perda de calor da água usando a seguinte relação:

Onde

e

Aqui,  é o coeficiente de transferência de calor convectivo da superfície externa,  é a emissividade, é a é a constante de Boltzmann e é a temperatura circundante. Substituindo os termos da equação acima pelos dados obtidos, temos:

Assim, a taxa total de perda de calor da água é .

b) Podemos calcular a temperatura de saída da água aplicando a equação do balanço energético.

Aqui  é a temperatura média de saída do tubo. Substituindo os termos da equação acima pelos dados obtidos, temos:

Assim, a temperatura de saída da água é .

Além disso, nossa temperatura média assumida é correta, pois não há muita diferença entre a temperatura de entrada e saída.