Considere uma placa vertical de de comprimento a na água a . Determine a velocidade de movimento forçado acima da qual a transferência de calor por convecção natural é desprezível.
Passo 1
Dados fornecidos:
Comprimento da placa:
Temperatura da placa:
Temperatura do ar exterior:
Premissas:
1) Existem condições operacionais estáveis.
Passo 2
Podemos fazer o seguinte esquema para exemplificar a placa:
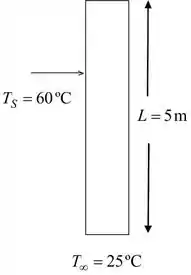
Passo 3
Para resolver essa questão, podemos começar calculando a temperatura do filme. Assim temos:
Com a temperatura de filme, podemos obter as propriedades da água na tabela A-9. Assim temos:
Coeficiente de expansão volumétrico:
Viscosidade dinâmica:
Densidade:
Assim, temos que a viscosidade cinemática pode ser dada pela seguinte relação:
Para a placa vertical o comprimento característico é igual ao comprimento.
Passo 4
Com os dados obtidos nos passos anteriores, podemos calcular o Número Grashof usando a seguinte relação:
Substituindo os termos da equação pelos dados obtidos, temos:
Vamos precisar calcular também o Número de Reynolds usando a seguinte relação:
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 5
No livro, podemos encontrar que a convecção natural é desprezível se a razão entre o número de Grashof e o quadrado do número de Reynolds for menor que . Podemos usar essa relação para encontrar a velocidade mínima do movimento forçado acima da qual a transferência de calor por convecção natural é desprezível.
Substituindo os termos da equação pelos dados obtidos, temos:
Portanto, a velocidade deve ser .