Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 8

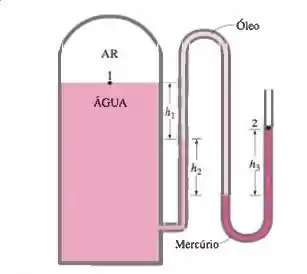
A água de um tanque é pressurizada a ar, e a pressão é medida por um manômetro de vários fluidos, como mostra a figura. Determine a pressão manométrica do ar no tanque se h 1 = 0,2   m , h 2 = 0,3   m e h 3 = 0,46   m . Tome as densidades da água, do óleo e do mercúrio como 1000 k g m 3 , 850 k g m 3   e   13600 k g m 3 respectivamente.

Passo 1

Bora lá! A questão ta pedindo a pressão manométrica do ponto 1, ou seja, a pressão do Ar sem considerar a pressão atmosférica, vamos chamar ela de P 1 .

O enunciado deu pra a gente as alturas h 1 = 0,2   m , h 2 = 0,3   m e h 3 = 0,46   m e as densidades ρ A = 1000 k g m 3 , ρ O = 850 k g m 3   e   ρ H g = 13600 k g m 3 .

Pra ajudar a gente tem esse desenhozinho:

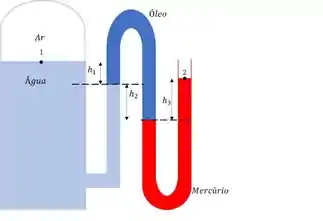
Um mesmo líquido em uma mesma altura tem a mesma pressão. Certo?! Então onde tem essa linha tracejada no nosso esqueminha são pontos que a gente vai usar para equiparar as pessões. Beleza?

Vamos então definir que na fronteira entre a água e o óleo a nossa pressão vai ser P A O , e na fronteira entre o óleo e o mercúrio a pressão vai ser P O H g .

Passo 2

Vamos começar do ponto entre o óleo e a água, onde a gente tem P A O :

P A O = ρ A g h 1 + P 1

Agora vamos ver o ponto entre o óleo e o mercúrio:

P O H g = ρ O g h 2 + P A O

E:

P O H g = ρ H g g h 3 + P 2

Passo 3

Agora podemos igualar as duas equações de P O H g :

ρ O g h 2 + P A O = ρ H g g h 3 + P 2

Agora substituindo P A O :

ρ O g h 2 + ρ A g h 1 + P 1 = ρ H g g h 3 + P 2

Mas P 2 = P a t m e aqui o que a gente quer é a pressão manométrica do ponto 1, logo o que a gente quer é P 1 - P a t m :

P 1 - P 2 = ρ H g g h 3 - ρ O g h 2 - ρ A g h 1

Vamos colocar esse g em evidência e chamar P 1 - P 2   de P 1 M A N :

P 1 M A N = g ( ρ H g h 3 - ρ O h 2 - ρ A h 1 )

Agora, finalmente substituindo:

P 1 M A N = 9,81 × 13600 × 0,46 - 850 × 0,3 - 1000 × 0,2

Agora é só calcular!

P 1 M A N = 56,9   k P a  

Resposta

P 1 M A N = 56,9   k P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um líquido, integre a relação hidrostática, Equação (2.12), considerando que o módulo de elasticidade volumétrico isentrópico, B = ρ δ p δ ρ s , seja constante – veja a Equação (9.18). Encontre u
Um tanque fechado contém 1,5 m de óleo SAE 30, 1 m de água, 20 cm de mercúrio e um espaço de ar no topo, tudo a 20 °C. A pressão absoluta no fundo do tanque é de 60 kPa. Qual é a pressão no espaço de
The system in Fig. P2.41 is at 208C. Compute the pressureat point A in lbf/ft2 absolute.
La Paz, Bolivia, is at an altitude of approximately12,000 ft. Assume a standard atmosphere. How highwould the liquid rise in a methanol barometer, assumedat 208C?
The Hoover Dam, in Arizona, encloses Lake Mead,which contains 10 trillion gallons of water. The dam is1200 ft wide and the lake is 500 ft deep. (a) Estimate thehydrostatic force on the dam, in MN. (b)